Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T02:23:51.660Z Has data issue: false hasContentIssue false
  • English
  • Français

Acoustic streaming in Maxwell fluids generated by standing waves in two-dimensional microchannels

Published online by Cambridge University Press:  06 January 2022

C. Vargas Open the ORCID record for C. Vargas [Opens in a new window] ,
I. Campos-Silva ,
F. Méndez Open the ORCID record for F. Méndez [Opens in a new window] ,
J. Arcos Open the ORCID record for J. Arcos [Opens in a new window]  and
O. Bautista Open the ORCID record for O. Bautista [Opens in a new window]
C. Vargas
Affiliation:
ESIME Zacatenco, Instituto Politécnico Nacional, Calz. Ticoman 600, San José Ticoman, Del. Gustavo A. Madero, Ciudad de México 07738, Mexico
I. Campos-Silva
Affiliation:
ESIME Zacatenco, Instituto Politécnico Nacional, Calz. Ticoman 600, San José Ticoman, Del. Gustavo A. Madero, Ciudad de México 07738, Mexico
F. Méndez
Affiliation:
Universidad Nacional Autónoma de México, Coyoacan, Ciudad de México 04510, Mexico
J. Arcos
Affiliation:
ESIME Azcapotzalco, Instituto Politécnico Nacional, Av. de las Granjas 682, Col. Santa Catarina, Azcapotzalco, Ciudad de México 02250, Mexico
O. Bautista*
Affiliation:
ESIME Azcapotzalco, Instituto Politécnico Nacional, Av. de las Granjas 682, Col. Santa Catarina, Azcapotzalco, Ciudad de México 02250, Mexico
*
†Email address for correspondence: obautista@ipn.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

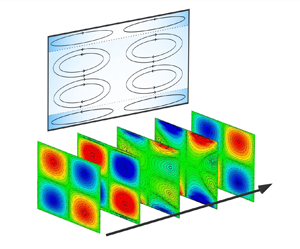
In this work, a semianalytic solution for the acoustic streaming phenomenon, generated by standing waves in Maxwell fluids through a two-dimensional microchannel (resonator), is derived. The mathematical model is non-dimensionalized and several dimensionless parameters that characterize the phenomenon arise: the ratio between the oscillation amplitude of the resonator and the half-wavelength ($\eta =2A/\lambda _{a}$); the product of the fluid relaxation time times the angular frequency known as the Deborah number ($De=\lambda _{1}\omega$); the aspect ratio between the microchannel height and the wavelength ($\epsilon =2 H_{0}/\lambda _{a}$); and the ratio between half the height of the microchannel and the thickness of the viscous boundary layer ($\alpha =H_{0}/\delta _{\nu }$). In the limit when $\eta \ll 1$, we obtain the hydrodynamic behaviour of the system using a regular perturbation method. In the present work, we show that the acoustic streaming speed is proportional to $\alpha ^{2.65}De^{1.9}$, and the acoustic pressure varies as $\alpha ^{6/5}De^{1/2}$. Also, we have found that the growth of inner vortex is due to convective terms in the Maxwell rheological equation. Furthermore, the velocity antinodes show a high dependency on the Deborah number, highlighting the fluid's viscoelastic properties and the appearance of resonance points. Due to the limitations of perturbation methods, we will only analyse narrow microchannels.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Micro-/Nano-fluid dynamics: Microscale transport Non-Newtonian Flows: Viscoelasticity
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 933 , 25 February 2022 , A59
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, D.A., Tannehill, J.C. & Pletcher, R.H. 1984 Computational Fluid Mechanics and Heat Transfer, vol. 1, chap. 3, pp. 45–76. Hemisphere Pub. Corp.Google Scholar
Antfolk, M. & Laurell, T. 2017 Continuous flow microfluidic separation and processing of rare cells and bioparticles found in blood. A review. Anal. Chim. Acta 965, 9–35.CrossRefGoogle ScholarPubMed
Antfolk, M. & Laurell, T. (Ed.) 2019 Acoustofluidic Blood Component Preparation and Processing in Medical Applications. Springer.CrossRefGoogle Scholar
Assche, D.V., Reithuber, E., Qiu, W., Laurell, T., Henriques-Normark, B., Mellroth, P., Ohlsson, P. & Augustsson, P. 2020 Gradient acoustic focusing of sub-micron particles for separation of bacteria from blood lysate. Sci. Rep. 10, 3670.CrossRefGoogle ScholarPubMed
Bach, J.S. & Bruus, H. 2020 Theory of acoustic trapping of microparticles in capillary tubes. Phys. Rev. E 101 (2), 023107.CrossRefGoogle ScholarPubMed
Baltean-Carles, D., Daru, V., Weisman, C., Tabakova, S. & Bailliet, H. 2019 An unexpected balance between outer Rayleigh streaming sources. J. Fluid Mech. 867, 985–1011.CrossRefGoogle Scholar
Bender, C.M. & Orszag, S.A. 2013 Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer Science and Business.Google Scholar
Bernoulli, D. 1738 Hydrodynamica, sive de viribus et motibus fluidorum commentarii. Johannis Reinholdi Dulseckeri.Google Scholar
Bird, R.B., Armstrong, R.C. & Hassager, O. 1987 Dynamics of Polymeric Liquids. Volume 1. Fluid Mechanics. John Wiley and Sons.Google Scholar
Bruus, H. 2008 Theoretical Microfluidics, vol. 1, chap. 15, pp. 255–272. Oxford University Press.Google Scholar
Bruus, H. 2012 a Acoustofluidics 2: perturbation theory and ultrasound resonance modes. Lab on a Chip 12, 20–28.CrossRefGoogle ScholarPubMed
Bruus, H. 2012 b Acoustofluidics 7: the acoustic radiation force on small particles. Lab on a Chip 12, 1014–1022.CrossRefGoogle ScholarPubMed
Chan, P.C.-H. & Leal, L.G. 1979 The motion of a deformable drop in a second-order fluid. J. Fluid Mech. 92, 131–170.CrossRefGoogle Scholar
Chang, C. & Schowalter, W.R. 1979 Secondary flow in the neighborhood of a cylinder oscillating in a viscoelastic fluid. J. Non-Newtonian Fluid Mech. 6, 47–67.CrossRefGoogle Scholar
Christakou, A.E., Ohlin, M., Vanherberghen, B., Khorshidi, M.A., Kadri, N., Frisk, T., Wiklund, M. & Onfelt, B. 2013 Live cell imaging in a micro-array of acoustic traps facilitates quantification of natural killer cell heterogeneity. Integr. Biol. 5, 712–719.CrossRefGoogle Scholar
Clausius, R. 1862 Ueber die wärmeleitung gasförmiger körper. Ann. Der Phys. Chem. 1, 299–340.Google Scholar
Crowl, L. & Fogelson, L. 2011 Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions. J. Fluid Mech. 676, 348–375.CrossRefGoogle Scholar
Eckart, C. 1948 Vortices and streams caused by sound waves. Phys. Rev. 73, 68–76.CrossRefGoogle Scholar
Faraday, M. 1837 On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Phil. Trans. R. Soc. Lond. 121, 299–340.Google Scholar
Hamilton, M.F., Ilinskii, Y.A. & Zabolotskaya, E.A. 2002 Nonlinear two-dimensional model for thermoacoustic engines. Acoust. Soc. Am. 111, 2076–2086.CrossRefGoogle ScholarPubMed
Hamilton, M.F., Ilinskii, Y.A. & Zabolotskaya, E.A. 2003 a Acoustic streaming generated by standing waves in two-dimensional channels of arbitrary width. Acoust. Soc. Am. 113, 153–160.CrossRefGoogle ScholarPubMed
Hamilton, M.F., Ilinskii, Y.A. & Zabolotskaya, E.A. 2003 b Thermal effects on acoustic streaming in standing waves. Acoust. Soc. Am. 114, 3092–3101.CrossRefGoogle ScholarPubMed
Hammarstrom, B., Laurell, T. & Nilsson, J. 2012 Seed particle-enabled acoustic trapping of bacteria and nanoparticles in continuous flow systems. Lab on a Chip 21, 4296–4304.CrossRefGoogle Scholar
Hasgall, P.A., Gennaro, F.D., Baumgartner, C., Neufeld, E., Lloyd, B., Gosselin, M.C., Payne, D., Klingenbock, A. & Kuster, N. 2018 IT'IS database for thermal and electromagnetic parameters of biological tissues. Version 4.0. Available from http://itis.swiss/database.Google Scholar
Jakobsson, O., Grenvall, C., Nordin, M., Evander, M. & Laurell, T. 2014 Acoustic actuated fluorescence activated sorting of microparticles. Lab on a Chip 14, 1943–1950.CrossRefGoogle ScholarPubMed
Joule, J.P. 1848 Some remarks on heat and the constitution of elastic fluids. Mem. Manchester Lit. Phil. Soc. 14, 107–114.Google Scholar
Ku, A., Ravi, N., Yang, M., Evander, M., Laurell, T., Lilja, H. & Ceder, Y. 2019 A urinary extracellular vesicle microrna biomarker discovery pipeline; from automated extracellular vesicle enrichment by acoustic trapping to microrna sequencing. Biomicrofluidics 14, 0217507.Google ScholarPubMed
Landau, L.D. & Lifshitz, E.M. (ed.) 1987 Fluid Mechanics. Pergamon.Google Scholar
Laurell, T., Petersson, F. & Nilsson, A. 2007 Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 36, 492–506.CrossRefGoogle ScholarPubMed
Lee, P.J. & Hung, P.J. 2005 Microfluidic application-specific integrated device for monitoring direct cell-cell communication via gap junctions between individual cell pairs. Appl. Phys. Lett. 86, 223902.CrossRefGoogle Scholar
Lighthill, J. 1978 Acoustic streaming. J. Sound Vib. 61, 391–418.CrossRefGoogle Scholar
Macosko, C.W. 1994 Rheology: Principles, Measurements, and Applications. pp. 135–172. Wiley-VCH, Inc.Google Scholar
Maxwell, J.C. 1867 On the dynamical theory of gases. Phil. Trans. R. Soc. Lond. 157, 49–88.Google Scholar
Newton, I. 1687 Philosophiae Naturalis Principia Mathematica. Mathematical Principles of Natural Philosophy. London: Streater J.CrossRefGoogle Scholar
Nyborg, W.L. 1965 Acoustic streaming. In Physical Acoustics (ed. Mason, W.P.), vol. 2B, pp. 265–331. Academic Press.Google Scholar
Olm, F., Urbansky, A., Dykes, J.H., Laurell, T. & Scheding, S. 2019 Label-free neuroblastoma cell separation from hematopoietic progenitor cell products using acoustophoresis-towards cell processing of complex biological samples. Sci. Rep. 9, 8777.CrossRefGoogle ScholarPubMed
Ortín, J. 2019 Stokes layers in oscillatory flows of viscoelastic fluids. Phil. Trans. R. Soc. Lond. A 378, 20190521.Google Scholar
Oyama, T., Imashiro, C., Kuriyama, T., Usui, H., Ando, K., Azuma, T., Morikawa, A., Kodeki, K., Takahara, O. & Takemura, K. 2021 Acoustic streaming induced by MHz-frequency ultrasound extends the volume limit of cells suspension culture. J. Acoust. Soc. Am. 149, 4180–4189.CrossRefGoogle ScholarPubMed
Qi, Q.M. & Shaqfeh, E.S.G. 2018 Time-dependent particle migration and margination in the pressure-driven channel flow of blood. Phys. Rev. Fluids 3, 034302.CrossRefGoogle Scholar
Rayleigh, Lord 1884 On the circulation of air observed in Kundts tubes, and on some allied acoustical problems. Phil. Trans. R. Soc. Lond. 175, 1–21.Google Scholar
Rednikov, A.Y. & Sadhal, S.S. 2011 Acoustic-steady streaming from a motionless boundary and related phenomena: generalized treatment of the inner streaming and examples. J. Fluid Mech. 667, 426–462.CrossRefGoogle Scholar
Riley, N. 2001 Steady streaming. Annu. Rev. Fluid Mech. 33 (1), 43–65.CrossRefGoogle Scholar
Sadhal, S.S. 2012 Analysis of Acoustic Streaming by Perturbation Methods, vol. 12, chap. 13, pp. 2292–2300. Lab Chip.CrossRefGoogle Scholar
Schlichting, H. 1932 Berechnung ebener periodischer grenzschicht-strommungen [calculation of plane periodic boundary layer streaming]. Phys. Zcit. 33, 327–335.Google Scholar
Skelley, A.M., Kirak, O., Suh, H., Jaenisch, R. & Voldman, J. 2009 Microfluidic control of cell pairing and fusion. Nat. Meth. 6, 147–152.CrossRefGoogle ScholarPubMed
Sritharan, K., Strobl, C.J., Schneider, M.F., Wixforth, A. & Guttenberg, Z. 2006 Acoustic mixing at low Reynolds numbers. Appl. Phys. Lett. 88, 054102.CrossRefGoogle Scholar
Stokes, G.G. 1851 a An examination of the possible effect of radiation of heat on the propagation of sound. Phil. Mag. 4, 305–317.CrossRefGoogle Scholar
Stokes, G.G. 1851 b On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Cambridge Philosophical Society.Google Scholar
Stuart, J.T. 1966 Double boundary layers in oscillatory viscous flow. J. Fluid Mech. 24, 673–687.CrossRefGoogle Scholar
Tanner, R.I. (Ed.) 1985 Engineering Rheology. Oxford Engineering Science Series. Clarendon.Google Scholar
Vanherbeghen, B., Manneberg, O., Christakou, A., Frisk, T., Ohlin, M., Hertz, H.M., Onfelt, B. & Wiklund, M. 2010 Ultrasound-controlled cell aggregation in a multi-well chip. Lab on a Chip 10, 2727–2732.CrossRefGoogle Scholar
Wang, C. 1968 On high-frequency oscillatory viscous flows. J. Fluid Mech. 32, 55–68.CrossRefGoogle Scholar
Westervelt, P.J. 1953 The theory of steady rotational flow generated by sound field. J. Acoust. Soc. Am. 25, 60–67.CrossRefGoogle Scholar
White, F.M. 2006 Viscous Fluid Flow, 3rd edn, vol. 1, chap. 7, pp. 511–514. McGraw-Hill.Google Scholar
Wohl, P.R. & Rubinow, S.I. 1974 The transverse force on a drop in an unbounded parabolic flow. J. Fluid Mech. 62, 185–207.CrossRefGoogle Scholar
Yalamanchili, R.V.S. & Benzkofer, P.D. 1973 Unsteady compressible boundary layers with arbitrary pressure gradients. AIAA Paper 73-132.CrossRefGoogle Scholar