Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T23:07:11.478Z Has data issue: false hasContentIssue false
  • English
  • Français

Aerodynamic noise from a poroelastic edge with implications for the silent flight of owls

Published online by Cambridge University Press:  16 April 2013

Justin W. Jaworski  and
N. Peake
Justin W. Jaworski*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
N. Peake
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: J.W.Jaworski@damtp.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The interaction of a turbulent eddy with a semi-infinite poroelastic edge is examined with respect to the effects of both elasticity and porosity on the efficiency of aerodynamic noise generation. 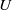The scattering problem is solved using the Wiener–Hopf technique to identify the scaling dependence of the resulting aerodynamic noise on plate and flow properties, including the dependence on a characteristic flow velocity $U$. Special attention is paid to the limiting cases of porous-rigid and impermeable–elastic plate conditions. Asymptotic analysis of these special cases reveals parametric limits where the far-field acoustic power scales like 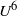${U}^{6} $ for a porous edge, and a new finite range of 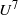${U}^{7} $ behaviour is found for an elastic edge, to be compared with the well-known 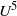${U}^{5} $ dependence for a rigid impermeable edge. Further numerical results attempt to address how trailing-edge noise may be mitigated by porosity and flexibility and seek to deepen the understanding of how owls hunt in acoustic stealth.

JFM classification

Acoustics: Aeroacoustics Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 456 - 479
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amiet, R. K. 1975 Acoustic radiation from an airfoil in a turbulent stream. J. Sound Vib. 41 (4), 407–420.CrossRefGoogle Scholar
Barone, J. R. & Schmidt, W. F. 2005 Polyethylene reinforced with keratin fibres obtained from chicken feathers. Compos. Sci. Technol. 65, 173–181.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bers, A. 1983 Space–time evolution of plasma instabilities – absolute and convective. In Basic Plasma Physics (ed. Galeev, A. A. & Sudan, R. N.), Handbook of Plasma Physics, vol. 1, North-Holland.Google Scholar
Bliss, D. B. 1982 Study of bulk reacting porous sound absorbers and a new boundary condition for thin porous layers. J. Acoust. Soc. Am. 71 (3), 533–545.Google Scholar
Bonser, R. & Purslow, P. 1995 The Young’s modulus of feather keratin. J. Expl Biol. 198, 1029–1033.CrossRefGoogle ScholarPubMed
Briggs, R. J. 1964 Electron-Stream Interaction with Plasmas. MIT.Google Scholar
Bull, E. L. & Duncan, J. R. 1993 Great Gray Owl: Strix Nebulosa. American Orinthologists’ Union.Google Scholar
Cannell, P. A. 1975 Edge scattering of aerodynamic sound by a lightly loaded elastic half-plane. Proc. R. Soc. Lond. A 347 (1649), 213–238.Google Scholar
Cannell, P. A. 1976 Acoustic edge scattering by a heavily loaded elastic half-plane. Proc. R. Soc. Lond. A 350 (1660), 71–89.Google Scholar
Carpenter, T. W. 1992 Utility of wing length, tail length and tail barring in determining the sex of Barred Owls collected in Michigan and Minnesota. The Condor 94, 794–795.Google Scholar
Chong, T. P., Joseph, P. F. & Gruber, M. 2013 Airfoil self noise reduction by non-flat plate type trailing edge serrations. Appl. Acoust. 74, 607–613.CrossRefGoogle Scholar
Crighton, D. G. 1972 Acoustic edge scattering of elastic surface waves. J. Sound Vib. 22 (1), 25–32.Google Scholar
Crighton, D. G. 1991 Airframe noise. In Aerodynamic Theory: A General Review of Progress. Volume 1: Noise Sources (ed. Hubbard, H. H.). NASA Langley Research Center.Google Scholar
Crighton, D. G. 2001 Asymptotic factorization of Wiener–Hopf kernels. Wave Motion 33, 51–65.Google Scholar
Crighton, D. G. & Leppington, F. G. 1970 Scattering of aerodynamic noise by a semi-infinite compliant plate. J. Fluid Mech. 43 (4), 721–736.CrossRefGoogle Scholar
Crighton, D. G. & Leppington, F. G. 1973 Singular perturbation methods in acoustics: diffraction by a plate of finite thickness. Proc. R. Soc. Lond. A 335 (1602), 313–339.Google Scholar
Curle, N. 1955 The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. A 231 (1187), 505–514.Google Scholar
Dassen, T., Parchen, R., Bruggeman, J. & Hagg, F. 1996 Results of a wind tunnel study on the reduction of airfoil self-noise by the application of serrated blade trailing edges. In European Union Wind Energy Conference and Exhibition, Gothenburg, Sweden, pp. 800–803.Google Scholar
Earhart, C. M. & Johnson, N. K. 1970 Size dimorphism and food habits of North American owls. The Condor 72, 251–264.CrossRefGoogle Scholar
Ffowcs Williams, J. E. 1972 The acoustics of turbulence near sound-absorbent liners. J. Fluid Mech. 51 (4), 737–749.CrossRefGoogle Scholar
Ffowcs Williams, J. E. & Hall, L. E. 1970 Aerodynamic sound generation by turbulent flow in the vicinity of a scattering half plane. J. Fluid Mech. 40 (4), 657–670.Google Scholar
Geyer, T., Sarradj, E. & Fritzsche, C. 2010 Measurement of the noise generation at the trailing edge of porous airfoils. Exp. Fluids 48 (2), 291–308.Google Scholar
Godfrey, W. E. & Crosby, J. A. 1986 The Birds of Canada. National Museum of Natural Sciences.Google Scholar
Graham, R. R. 1934 The silent flight of owls. J. R. Aero. Soc. 38, 837–843.CrossRefGoogle Scholar
Gruschka, H. D., Borchers, I. U. & Coble, J. G. 1971 Aerodynamic noise produced by a gliding owl. Nature 233, 409–411.Google Scholar
Hayden, R. E. 1976 Reduction of noise from airfoils and propulsive lift systems using variable impedance systems. AIAA Paper 1976-500.Google Scholar
Hayward, G. D. & Hayward, P. H. 1991 Body measurements of Boreal Owls in Idaho and a discriminant model to determine sex of live specimens. Wilson Bull. 103 (3), 497–500.Google Scholar
Herr, M. 2007 Design criteria for low-noise trailing-edges. AIAA Paper 2007-3470.Google Scholar
Herr, M. & Dobrzynski, W. 2005 Experimental investigations in low-noise trailing-edge design. AIAA J. 43 (6), 1167–1175.CrossRefGoogle Scholar
Howe, M. S. 1978 A review of the theory of trailing edge noise. J. Sound Vib. 61 (3), 437–465.CrossRefGoogle Scholar
Howe, M. S. 1979a On the added mass of a perforated shell, with application to the generation of aerodynamic sound by a perforated trailing edge. Proc. R. Soc. Lond. A 365 (1721), 209–233.Google Scholar
Howe, M. S. 1979b On the theory of unsteady high Reynolds number flow through a circular aperture. Proc. R. Soc. Lond. A 366 (1725), 205–223.Google Scholar
Howe, M. S. 1984 On the generation of sound by turbulent boundary layer flow over a rough wall. Proc. R. Soc. Lond. A 395 (1809), 247–263.Google Scholar
Howe, M. S. 1991a Aerodynamic noise of a serrated trailing edge. J. Fluids Struct. 5 (1), 33–45.Google Scholar
Howe, M. S. 1991b Noise produced by a sawtooth trailing edge. J. Acoust. Soc. Am. 90 (1), 482–487.Google Scholar
Howe, M. S. 1992 Sound produced by an aerodynamic source adjacent to a partly coated, finite elastic plate. Proc. R. Soc. Lond. A 436 (1897), 351–372.Google Scholar
Howe, M. S. 1993 Structural and acoustic noise produced by turbulent flow over an elastic trailing edge. Proc. R. Soc. Lond. A 442 (1916), 533–554.Google Scholar
Howe, M. S. 1998 Acoustics of Fluid-Structure Interactions. Cambridge University Press.Google Scholar
Howe, M. S. 2001 Edge-source acoustic Green’s function for an airfoil of arbitrary chord, with application to trailing-edge noise. Q. J. Mech. Appl. Maths 54 (1), 139–155.Google Scholar
Howe, M. S., Scott, M. I. & Sipcic, S. R. 1996 The influence of tangential mean flow on the Rayleigh conductivity of an aperture. Proc. R. Soc. Lond. A 452 (1953), 2303–2317.Google Scholar
Hughes, I. J. & Dowling, A. P. 1990 The absorption of sound by perforated linings. J. Fluid Mech. 218, 299–335.Google Scholar
Johnsgard, P. A. 2002 North American Owls: Biology and Natural History, 2nd edn. Smithsonian Institution.Google Scholar
Jones, L. E. & Sandberg, R. D. 2012 Acoustic and hydrodynamic analysis of the flow around an aerofoil with trailing-edge serrations. J. Fluid Mech. 706, 295–322.CrossRefGoogle Scholar
Khorrami, M. R. & Choudhari, M. M. 2003 Application of passive porous treatment for slat trailing edge noise. NASA Tech. Rep. TM-2003-212416.Google Scholar
Kranzer, H. C. 1968 Asymptotic factorization in nondissipative Wiener–Hopf problems. J. Math. Mech. 17, 577–600.Google Scholar
Kranzer, H. C. & Radlow, J. 1962 Asymptotic factorization for perturbed Wiener–Hopf problems. J. Math. Anal. Appl. 4, 240–256.CrossRefGoogle Scholar
Kranzer, H. C. & Radlow, J. 1965 An asymptotic method for solving perturbed Wiener–Hopf problems. J. Math. Mech. 14, 41–59.Google Scholar
Kroeger, R. A., Gruschka, H. D. & Helvey, T. C. 1972 Low speed aerodynamics for ultra-quiet flight. Tech. Rep. AFFDL-TR-71-75. Air Force Flight Dynamics Laboratory, Wright-Patterson AFB.Google Scholar
Leppington, F. G. 1977 The effective compliance of perforated screens. Mathematika 24, 199–215.Google Scholar
Leppington, F. G. 1990 The effective boundary conditions for a perforated elastic sandwich panel in a compressible fluid. Proc. R. Soc. Lond. A 427 (1873), 385–399.Google Scholar
Lighthill, M. J. 1952 On sound generated aerodynamically. Part 1. General theory. Proc. R. Soc. Lond. A 211 (1107), 564–587.Google Scholar
Lilley, G. M. 1998 A study of the silent flight of the owl. AIAA Paper 1998-2340.Google Scholar
Marti, C. D. 1990 Sex and age dimorphism in the Barn Owl and a test of mate choice. The Auk 107, 246–254.CrossRefGoogle Scholar
Martinez, R. & Widnall, S. E. 1980 Unified aerodynamic-acoustic theory for a thin rectangular wing encountering a gust. AIAA J. 18 (6), 636–645.Google Scholar
Moreau, D. J., Brooks, L. A. & Doolan, C. J. 2012 On the noise reduction mechanism of a flat plate serrated trailing edge at low-to-moderate Reynolds number. AIAA Paper 2012-2186.CrossRefGoogle Scholar
Nelson, P. A. 1982 Noise generated by flow over perforated surfaces. J. Sound Vib. 83 (1), 11–26.CrossRefGoogle Scholar
Noble, B. 1988 Methods Based on the Wiener–Hopf Technique for the Solution of Partial Differential Equations. Chelsea.Google Scholar
Oerlemans, S., Fisher, M., Maeder, T. & Kögler, K. 2009 Reduction of wind turbine noise using optimized airfoils and trailing-edge serrations. AIAA J. 47 (6), 1470–1481.CrossRefGoogle Scholar
Peake, N. 2004 On the unsteady motion of a long fluid-loaded elastic plate with mean flow. J. Fluid Mech. 507, 335–366.CrossRefGoogle Scholar
Rains, C. R. 1998 Niche overlap, and nearest-neighbor distances of Northern Saw-whet Owls (aegolius acadicus) and Western Screech-owls (otus kennicottii) in southwestern Idaho. PhD thesis, Boise State University.Google Scholar
Rayleigh, Lord 1945 The Theory of Sound, vol. 2. Dover.Google Scholar
Rienstra, S. W. 2007 Acoustic scattering at a hard-soft lining transition in a flow duct. J. Engng Maths 59 (4), 451–475.CrossRefGoogle Scholar
Roger, M. & Moreau, S. 2005 Back-scattering correction and further extensions of Amiet’s trailing-edge noise model. Part 1. Theory. J. Sound Vib. 286, 477–506.Google Scholar
Sandberg, R. D. & Jones, L. E. 2011 Direct numerical simulations of low Reynolds number flow over airfoils with trailing-edge serrations. J. Sound Vib. 330, 3818–3831.Google Scholar
Sarradj, E., Fritzsche, C. & Geyer, T. 2011 Silent owl flight: flyover noise measurements. AIAA J. 49 (4), 769–779.Google Scholar
Snyder, N. F. & Wiley, J. W. 1976 Sexual Size Dimorphism in Hawks and Owls of North America (No. 20). American Orinthologists’ Union.Google Scholar
Timoshenko, S. 1940 Theory of Plates and Shells, 1st edn. McGraw-Hill.Google Scholar
Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. Parabolic.Google Scholar
Veitch, B. & Peake, N. 2008 Acoustic propagation and scattering in the exhaust flow from coaxial cylinders. J. Fluid Mech. 613, 275–307.CrossRefGoogle Scholar
Zwikker, C. & Kosten, C. W. 1949 Sound Absorbing Materials. Elsevier.Google Scholar