Article contents
Ageostrophic instability in rotating, stratified interior vertical shear flows
Published online by Cambridge University Press: 19 August 2014
Abstract
The linear instability of several rotating, stably stratified, interior vertical shear flows  $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\overline{U}(z)$ is calculated in Boussinesq equations. Two types of baroclinic, ageostrophic instability, AI1 and AI2, are found in odd-symmetric
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\overline{U}(z)$ is calculated in Boussinesq equations. Two types of baroclinic, ageostrophic instability, AI1 and AI2, are found in odd-symmetric 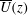 $\overline{U}(z)$ for intermediate Rossby number (
$\overline{U}(z)$ for intermediate Rossby number ( 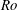 $\mathit{Ro}$ ). AI1 has zero frequency; it appears in a continuous transformation of the unstable mode properties between classic baroclinic instability (BCI) and centrifugal instability (CI). It begins to occur at intermediate
$\mathit{Ro}$ ). AI1 has zero frequency; it appears in a continuous transformation of the unstable mode properties between classic baroclinic instability (BCI) and centrifugal instability (CI). It begins to occur at intermediate 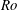 $\mathit{Ro}$ values and horizontal wavenumbers (
$\mathit{Ro}$ values and horizontal wavenumbers (  $k,l$ ) that are far from
$k,l$ ) that are far from 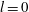 $l= 0$ or
$l= 0$ or 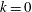 $k = 0$ , where the growth rate of BCI or CI is the strongest. AI1 grows by drawing kinetic energy from the mean flow, and the perturbation converts kinetic energy to potential energy. The instability AI2 has inertia critical layers (ICL); hence it is associated with inertia-gravity waves. For an unstable AI2 mode, the coupling is either between an interior balanced shear wave and an inertia-gravity wave (BG), or between two inertia-gravity waves (GG). The main energy source for an unstable BG mode is the mean kinetic energy, while the main energy source for an unstable GG mode is the mean available potential energy. AI1 and BG type AI2 occur in the neighbourhood of
$k = 0$ , where the growth rate of BCI or CI is the strongest. AI1 grows by drawing kinetic energy from the mean flow, and the perturbation converts kinetic energy to potential energy. The instability AI2 has inertia critical layers (ICL); hence it is associated with inertia-gravity waves. For an unstable AI2 mode, the coupling is either between an interior balanced shear wave and an inertia-gravity wave (BG), or between two inertia-gravity waves (GG). The main energy source for an unstable BG mode is the mean kinetic energy, while the main energy source for an unstable GG mode is the mean available potential energy. AI1 and BG type AI2 occur in the neighbourhood of  $A-S= 0$ (a sign change in the difference between absolute vertical vorticity and horizontal strain rate in isentropic coordinates; see McWilliams et al., Phys. Fluids, vol. 10, 1998, pp. 3178–3184), while GG type AI2 arises beyond this condition. Both AI1 and AI2 are unbalanced instabilities; they serve as an initiation of a possible local route for the loss of balance in 3D interior flows, leading to an efficient energy transfer to small scales.
$A-S= 0$ (a sign change in the difference between absolute vertical vorticity and horizontal strain rate in isentropic coordinates; see McWilliams et al., Phys. Fluids, vol. 10, 1998, pp. 3178–3184), while GG type AI2 arises beyond this condition. Both AI1 and AI2 are unbalanced instabilities; they serve as an initiation of a possible local route for the loss of balance in 3D interior flows, leading to an efficient energy transfer to small scales.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 13
- Cited by

