Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-14T04:55:39.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Amplitude modulation of all three velocity components in turbulent boundary layers

Published online by Cambridge University Press:  31 March 2014

K. M. Talluru ,
R. Baidya ,
N. Hutchins  and
I. Marusic
K. M. Talluru
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Melbourne, Victoria 3010, Australia
R. Baidya
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Melbourne, Victoria 3010, Australia
N. Hutchins*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Melbourne, Victoria 3010, Australia
I. Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: nhu@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

A combination of cross-wire probes with an array of flush-mounted skin-friction sensors are used to study the three-dimensional conditional organisation of large-scale structures in a high-Reynolds-number turbulent boundary layer. Previous studies have documented the amplitude modulation of small-scale motions in response to conditionally averaged large-scale events, but the data are largely restricted to the streamwise component of velocity alone. Here, we report results based on all three components of velocity and find that the small-scale spanwise and wall-normal fluctuations ($v$ and 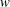$w$) and the instantaneous Reynolds shear stress (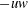$-{uw}$) are modulated in a very similar manner to that previously noted for the streamwise fluctuations ($u$). The envelope of the small scale fluctuations for all velocity components is well described by the large-scale component of the $u$ fluctuation. These results also confirm the conditional existence of roll modes associated with the very large-scale or ‘superstructure’ motions.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 746 , 10 May 2014 , R1
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I.2012 Measurements of streamwise and spanwise fluctuating velocity components in a high Reynolds number turbulent boundary layer. In Proc. 18th Australasian Fluid Mech. Conference.Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.CrossRefGoogle Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23 (6), 061701.CrossRefGoogle Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.CrossRefGoogle Scholar
Chauhan, K. A., Nagib, H. M. & Monkewitz, P. A. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.CrossRefGoogle Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. A 365, 647–664.CrossRefGoogle ScholarPubMed
Hutchins, N., Monty, J. P., Ganapathisubramani, B., NG, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Jacobi, I. & McKeon, B. J. 2013 Phase relationships between large and small scales in the turbulent boundary layer. Exp. Fluids 54 (3), 1–13.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.CrossRefGoogle ScholarPubMed
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the ${k}_{1}^{-1}$ law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.Google Scholar
Philip, J., Baidya, R., Hutchins, N., Monty, J. P. & Marusic, I. 2013 Spatial averaging of streamwise and spanwise velocity measurements in wall-bounded turbulence using v- and x-probes. Meas. Sci. Technol. 24, 115302.Google Scholar
Schlatter, P. & Örlü, R. 2010a Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010b Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22 (5), 051704.CrossRefGoogle Scholar
Sillero, J. A., Jimenez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to $\delta ^+ = 2000$ . Phys. Fluids 25 (10), 105102.CrossRefGoogle Scholar