Article contents
An experimental study of the free evolution of rotating, nonlinear internal gravity waves in a two-layer stratified fluid
Published online by Cambridge University Press: 21 February 2014
Abstract
The temporal evolution of nonlinear large-scale internal gravity waves, in a two-layer flow affected by background rotation, is studied via laboratory experiments conducted in a cylindrical tank, mounted on a rotating turntable. The internal wave field is excited by the relaxation of an initial forced tilt of the density interface (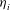 $\eta _{i}$), which generates internal waves, such as Kelvin and Poincaré waves, in response to rotation effects. The behaviour of
$\eta _{i}$), which generates internal waves, such as Kelvin and Poincaré waves, in response to rotation effects. The behaviour of 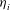 $\eta _{i}$, in the shore region, is analysed in terms of the background rotation and the nonlinear steepening of the basin-scale waves. The results show that the degeneration of the fundamental Kelvin wave into a solitary-type wave packet is caused by nonlinear steepening and it is influenced by the background rotation. In addition, the physical scales of the leading solitary-type wave are closer to Korteweg–de Vries theory as the rotation increases. Moreover, the nonlinear interaction between the Kelvin wave and the Poincaré wave can transfer energy to higher or lower frequencies than the frequency of the fundamental Kelvin wave, as a function of the background rotation. In particular, a specific normal mode in the off-shore region could be energized by this interaction. Finally, the bulk decay rate of the fundamental Kelvin wave,
$\eta _{i}$, in the shore region, is analysed in terms of the background rotation and the nonlinear steepening of the basin-scale waves. The results show that the degeneration of the fundamental Kelvin wave into a solitary-type wave packet is caused by nonlinear steepening and it is influenced by the background rotation. In addition, the physical scales of the leading solitary-type wave are closer to Korteweg–de Vries theory as the rotation increases. Moreover, the nonlinear interaction between the Kelvin wave and the Poincaré wave can transfer energy to higher or lower frequencies than the frequency of the fundamental Kelvin wave, as a function of the background rotation. In particular, a specific normal mode in the off-shore region could be energized by this interaction. Finally, the bulk decay rate of the fundamental Kelvin wave,  $\tau _{dk}$, was investigated. The results exhibit that
$\tau _{dk}$, was investigated. The results exhibit that 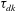 $\tau _{dk}$ is concordant with the Ekman damping time scale when there is no evidence of steepening in the basin-scale waves. However, as nonlinear processes increase,
$\tau _{dk}$ is concordant with the Ekman damping time scale when there is no evidence of steepening in the basin-scale waves. However, as nonlinear processes increase, 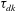 $\tau _{dk}$ shows a strong decrease. In this context, the nonlinear processes play an important role in the decay of the fundamental Kelvin wave, via the energy radiation to other modes. The results reported demonstrate that the background rotation and nonlinear processes are essential aspects in understanding the degeneration and the decay of large-scale internal gravity waves on enclosed basins.
$\tau _{dk}$ shows a strong decrease. In this context, the nonlinear processes play an important role in the decay of the fundamental Kelvin wave, via the energy radiation to other modes. The results reported demonstrate that the background rotation and nonlinear processes are essential aspects in understanding the degeneration and the decay of large-scale internal gravity waves on enclosed basins.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 15
- Cited by


