Article contents
Anisotropic wall permeability effects on turbulent channel flows
Published online by Cambridge University Press: 21 September 2018
Abstract
Streamwise–wall-normal ( $x$–
$x$–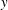 $y$) and streamwise–spanwise (
$y$) and streamwise–spanwise ( $x$–
$x$– $z$) plane measurements are carried out by planar particle image velocimetry for turbulent channel flows over anisotropic porous media at the bulk Reynolds number
$z$) plane measurements are carried out by planar particle image velocimetry for turbulent channel flows over anisotropic porous media at the bulk Reynolds number 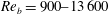 $Re_{b}=900{-}13\,600$. Three kinds of anisotropic porous media are constructed to form the bottom wall of the channel. Their wall permeability tensor is designed to have a larger wall-normal diagonal component (wall-normal permeability) than the other components. Those porous media are constructed to have three mutually orthogonal principal axes and those principal axes are aligned with the Cartesian coordinate axes of the flow geometry. Correspondingly, the permeability tensor of each porous medium is diagonal. With the
$Re_{b}=900{-}13\,600$. Three kinds of anisotropic porous media are constructed to form the bottom wall of the channel. Their wall permeability tensor is designed to have a larger wall-normal diagonal component (wall-normal permeability) than the other components. Those porous media are constructed to have three mutually orthogonal principal axes and those principal axes are aligned with the Cartesian coordinate axes of the flow geometry. Correspondingly, the permeability tensor of each porous medium is diagonal. With the  $x$–
$x$–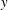 $y$ plane data, it is found that the turbulence level well accords with the order of the streamwise diagonal component of the permeability tensor (streamwise permeability). This confirms that the turbulence strength depends on the streamwise permeability rather than the wall-normal permeability when the permeability tensor is diagonal and the wall-normal permeability is larger than the streamwise permeability. To generally characterize those phenomena including isotropic porous wall cases, modified permeability Reynolds numbers are discussed. From a quadrant analysis, it is found that the contribution from sweeps and ejections to the Reynolds shear stress near the porous media is influenced by the streamwise permeability. In the
$y$ plane data, it is found that the turbulence level well accords with the order of the streamwise diagonal component of the permeability tensor (streamwise permeability). This confirms that the turbulence strength depends on the streamwise permeability rather than the wall-normal permeability when the permeability tensor is diagonal and the wall-normal permeability is larger than the streamwise permeability. To generally characterize those phenomena including isotropic porous wall cases, modified permeability Reynolds numbers are discussed. From a quadrant analysis, it is found that the contribution from sweeps and ejections to the Reynolds shear stress near the porous media is influenced by the streamwise permeability. In the  $x$–
$x$– $z$ plane data, although low- and high-speed streaks are also observed near the anisotropic porous walls, large-scale spanwise patterns appear at a larger Reynolds number. It is confirmed that they are due to the transverse waves induced by the Kelvin–Helmholtz instability. By the two-point correlation analyses of the fluctuating velocities, the spacing of the streaks and the wavelengths of the Kelvin–Helmholtz (K–H) waves are discussed. It is then confirmed that the transition point from the quasi-streak structure to the roll-cell-like structure is characterized by the wall-normal distance including the zero-plane displacement of the log-law velocity which can be characterized by the streamwise permeability. It is also confirmed that the normalized wavelengths of the K–H waves over porous media are in a similar range to that of the turbulent mixing layers irrespective of the anisotropy of the porous media.
$z$ plane data, although low- and high-speed streaks are also observed near the anisotropic porous walls, large-scale spanwise patterns appear at a larger Reynolds number. It is confirmed that they are due to the transverse waves induced by the Kelvin–Helmholtz instability. By the two-point correlation analyses of the fluctuating velocities, the spacing of the streaks and the wavelengths of the Kelvin–Helmholtz (K–H) waves are discussed. It is then confirmed that the transition point from the quasi-streak structure to the roll-cell-like structure is characterized by the wall-normal distance including the zero-plane displacement of the log-law velocity which can be characterized by the streamwise permeability. It is also confirmed that the normalized wavelengths of the K–H waves over porous media are in a similar range to that of the turbulent mixing layers irrespective of the anisotropy of the porous media.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 40
- Cited by


