Article contents
Axisymmetric travelling waves in annular sliding Couette flow at finite and asymptotically large Reynolds number
Published online by Cambridge University Press: 27 February 2013
Abstract
The relationship between numerical finite-amplitude equilibrium solutions of the full Navier–Stokes equations and nonlinear solutions arising from a high-Reynolds-number asymptotic analysis is discussed for a Tollmien–Schlichting wave-type two-dimensional vortical flow structure. The specific flow chosen for this purpose is that which arises from the mutual axial sliding of co-axial cylinders for which nonlinear axisymmetric travelling-wave solutions have been discovered recently by Deguchi & Nagata (J. Fluid Mech., vol. 678, 2011, pp. 156–178). We continue this solution branch to a Reynolds number 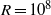 $R= 1{0}^{8} $ and confirm that the behaviour of its so-called lower branch solutions, which typically produce a smaller modification to the laminar state than the other solution branches, quantitatively agrees with the axisymmetric asymptotic theory developed in this paper. We further find that this asymptotic structure breaks down when the disturbance wavelength is comparable with
$R= 1{0}^{8} $ and confirm that the behaviour of its so-called lower branch solutions, which typically produce a smaller modification to the laminar state than the other solution branches, quantitatively agrees with the axisymmetric asymptotic theory developed in this paper. We further find that this asymptotic structure breaks down when the disturbance wavelength is comparable with 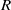 $R$ . The new structure which replaces it is investigated and the governing equations are derived and solved. The flow visualization of the resultant solutions reveals that they possess a streamwise localized structure, with the trend agreeing qualitatively with full Navier–Stokes solutions for relatively long-wavelength disturbances.
$R$ . The new structure which replaces it is investigated and the governing equations are derived and solved. The flow visualization of the resultant solutions reveals that they possess a streamwise localized structure, with the trend agreeing qualitatively with full Navier–Stokes solutions for relatively long-wavelength disturbances.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 9
- Cited by

