Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T22:41:51.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Coarsening and solidification via solvent-annealing in thin liquid films

Published online by Cambridge University Press:  16 April 2013

Tony S. Yu ,
Vladimir Bulović  and
A. E. Hosoi
Tony S. Yu*
Affiliation:
Brown School of Engineering, Brown University, Providence, RI 02906, USA
Vladimir Bulović
Affiliation:
Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
A. E. Hosoi
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: tonysyu@brown.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine solidification in thin liquid films produced by annealing amorphous 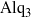${\mathrm{Alq} }_{3} $ (tris-(8-hydroxyquinoline) aluminium) in methanol vapour. Micrographs acquired during annealing capture the evolution of the film: the initially-uniform film breaks up into drops that coarsen, and single crystals of 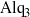${\mathrm{Alq} }_{3} $ nucleate randomly on the substrate and grow as slender ‘needles’. The growth of these needles appears to follow power-law behaviour, where the growth exponent, 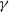$\gamma $, depends on the thickness of the deposited 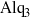${\mathrm{Alq} }_{3} $ film. The evolution of the thin film is modelled by a lubrication equation, and an advection–diffusion equation captures the transport of 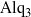${\mathrm{Alq} }_{3} $ and methanol within the film. We define a dimensionless transport parameter, $\alpha $, which is analogous to an inverse Sherwood number and quantifies the relative effects of diffusion- and coarsening-driven advection. For large $\alpha $-values, the model recovers the theory of one-dimensional, diffusion-driven solidification, such that 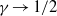$\gamma \rightarrow 1/ 2$. For low $\alpha $-values, the collapse of drops, i.e. coarsening, drives flow and regulates the growth of needles. Within this regime, we identify two relevant limits: needles that are small compared to the typical drop size, and those that are large. Both scaling analysis and simulations of the full model reveal that 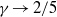$\gamma \rightarrow 2/ 5$ for small needles and 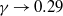$\gamma \rightarrow 0. 29$ for large needles.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Lubrication theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 69 - 90
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balluffi, R. W., Allen, S. M. & Carter, W. C. 2005 Kinetics of Materials, 1st edn. Wiley-Interscience.Google Scholar
Becerril, H. A., Roberts, M. E., Liu, Z. H., Locklin, J. & Bao, Z. N. 2008 High-performance organic thin-film transistors through solution-sheared deposition of small-molecule organic semiconductors. Adv. Mater. 20 (13), 2588–2594.CrossRefGoogle Scholar
Becker, J., Grun, G., Seemann, R., Mantz, H., Jacobs, K., Mecke, K. R. & Blossey, R. 2003 Complex dewetting scenarios captured by thin-film models. Nature Mater. 2 (1), 59–63.CrossRefGoogle ScholarPubMed
Bollinne, C., Cuenot, S., Nysten, B. & Jonas, A. M. 2003 Spinodal-like dewetting of thermodynamically-stable thin polymer films. Eur. Phys. J. E 12 (3), 389–395.CrossRefGoogle ScholarPubMed
Brinkmann, M., Wittmann, J. C., Chaumont, C. & Andrè, J. J. 1997 Effects of solvent on the morphology and crystalline structure of lithium phthalocyanine thin films and powders. Thin Solid Films 292 (1–2), 192–203.Google Scholar
Chen, W., Peng, Q. & Li, Y. 2008 Alq(3) nanorods: promising building blocks for optical devices. Adv. Mater. 20 (14), 2747–2750.Google Scholar
Cook, B. P., Bertozzi, A. L. & Hosoi, A. E. 2008 Shock solutions for particle–laden thin films. SIAM J. Appl. Maths 68 (3), 760–783.Google Scholar
Crank, J. 1975 Mathematics of Diffusion. Clarendon.Google Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81 (3), 1131–1198.Google Scholar
Dickey, K. C., Anthony, J. E. & Loo, Y. L. 2006 Improving organic thin-film transistor performance through solvent-vapour annealing of solution-processable triethylsilylethynyl anthradithiophene. Adv. Mater. 18 (13), 1721–1726.CrossRefGoogle Scholar
Glasner, K. B. & Witelski, T. P. 2003 Coarsening dynamics of dewetting films. Phys. Rev. E 67 (1, Part 2), 016302.Google Scholar
Glasner, K. B. & Witelski, T. P. 2005 Collision versus collapse of droplets in coarsening of dewetting thin films. Physica D 209 (1–4), 80–104.Google Scholar
Gomba, J. M. & Homsy, G. M. 2009 Analytical solutions for partially wetting two-dimensional droplets. Langmuir 25 (10), 5684–5691.Google Scholar
Gotze, W. & Voigtmann, T. 2003 Effect of composition changes on the structural relaxation of a binary mixture. Phys. Rev. E 67 (2), 021502.CrossRefGoogle ScholarPubMed
Granasy, L., Pusztai, T., Borzsonyi, T., Warren, J. A. & Douglas, J. F. 2004 A general mechanism of polycrystalline growth. Nature Mater. 3 (9), 645–650.CrossRefGoogle ScholarPubMed
Ishii, Y., Shimada, T., Okazaki, N. & Hasegawa, T. 2007 Wetting-dewetting oscillations of liquid films during solution-mediated vacuum deposition of rubrene. Langmuir 23 (12), 6864–6868.Google Scholar
Israelachvili, J. N. 1991 Intermolecular and Surface Forces, 2nd edn. Academic.Google Scholar
Kao, J. C. T., Golovin, A. A. & Davis, S. H. 2006 Rupture of thin films with resonant substrate patterning. J. Colloid Interface Sci. 303 (2), 532–545.Google Scholar
Langer, J. S. 1980 Instabilities and pattern-formation in crystal-growth. Rev. Mod. Phys. 52 (1), 1–28.Google Scholar
Lee, S., Yoo, P., Kwon, S. & Lee, H. 2004 Solvent-driven dewetting and rim instability. J. Chem. Phys. 121, 4346.Google Scholar
Liu, S., Wang, W. M., Briseno, A. L., Mannsfeld, S. C. B. & Bao, Z. 2009 Controlled deposition of crystalline organic semiconductors for field-effect-transistor applications. Adv. Mater 21 (12), 1217–1232.Google Scholar
de Luca, G., Liscio, A., Maccagnani, P., Nolde, F., Palermo, V., Mllen, K. & Samorï, P. 2007 Nucleation-governed reversible self-assembly of an organic semiconductor at surfaces: long-range mass transport forming giant functional fibres. Adv. Funct. Mater. 17 (18), 3791–3798.CrossRefGoogle Scholar
de Luca, G., Liscio, A., Nolde, F., Scolaro, L. M., Palermo, V., Mullen, K. & Samori, P. 2008 Self-assembly of discotic molecules into mesoscopic crystals by solvent-vapour annealing. Soft Matt. 4 (10), 2064–2070.CrossRefGoogle Scholar
Mascaro, D. J., Thompson, M. E., Smith, H. I. & Bulovic, V. 2005 Forming oriented organic crystals from amorphous thin films on patterned substrates via solvent-vapour annealing. Organic Electron. 6 (5–6), 211–220.Google Scholar
Miller, S., Fanchini, G., Lin, Y. Y., Li, C., Chen, C. W., Su, W. F. & Chhowalla, M. 2008 Investigation of nanoscale morphological changes in organic photovoltaics during solvent vapour annealing. J. Mater. Chem. 18 (3), 306–312.Google Scholar
Náraigh, L. & Thiffeault, J. 2007 Dynamical effects and phase separation in cooled binary fluid films. Phys. Rev. E 76 (3), 035303.Google Scholar
Naraigh, L. O. & Thiffeault, J. 2010 Nonlinear dynamics of phase separation in thin films. Nonlinearity 23 (7), 1559–1583.Google Scholar
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69 (3), 931–980.Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1992 Numerical Recipes in C: the Art of Scientific Computing. Cambridge University Press.Google Scholar
Rabani, E., Reichman, D. R., Geissler, P. L. & Brus, L. E. 2003 Drying-mediated self-assembly of nanoparticles. Nature 426 (6964), 271–274.Google Scholar
Sears, J. K. & Darby, J. R. 1982 Technology of Plasticizers. John Wiley & Sons.Google Scholar
Sharma, A. 1993 Relationship of thin film stability and morphology to macroscopic parameters of wetting in the apolar and polar systems. Langmuir 9 (3), 861–869.Google Scholar
Starov, V. & Velarde, M. 2009 Surface forces and wetting phenomena. J. Phys.: Condens. Matter 21 (46), 464121.Google Scholar
Teletzke, G. F., Davis, H. T. & Scriven, L. E. 1988 Wetting hydrodynamics. Rev. Phys. Appl. 23 (6), 989–1007.Google Scholar
Thiele, U. 2011 Note on thin film equations for solutions and suspensions. Eur. Phys. J.-Special Topics 197 (1), 213–220.Google Scholar
Tian, X., Fei, J., Pi, Z., Yang, C., Luo, D., Pei, F. & Zhang, L. 2006 Selective temperature physical vapour deposition route to tri(8-hydroquinoline)aluminum nanowires, nanowalls, nanoclusters and micro-spherical chains. Solid State Commun. 138 (10–11), 530–533.Google Scholar
Valli, A. M. P., Carey, G. F. & Coutinho, A. L. G. A. 2005 Control strategies for time step selection in finite element simulation of incompressible flows and coupled reaction-convection-diffusion processes. Intl J. Numer. Meth. Fluids 47 (3), 201–231.Google Scholar
Wettlaufer, J. S. & Worster, M. G. 2006 Premelting dynamics. Annu. Rev. Fluid Mech. 38, 427–452.Google Scholar
Xu, L., Shi, T. & An, L. 2008 The dewetting dynamics of the polymer thin film by solvent annealing. J. Chem. Phys. 129, 044904.Google Scholar
Yu, T. S. 2011 Solidification in a thin liquid film: growing ${\mathrm{Alq} }_{3} $ needles via methanol-vapour annealing. PhD thesis, MIT.Google Scholar
Zhou, J. J., Dupuy, B., Bertozzi, A. L. & Hosoi, A. E. 2005 Theory for shock dynamics in particle–laden thin films. Phys. Rev. Lett. 94 (11), 117803.CrossRefGoogle ScholarPubMed