Published online by Cambridge University Press: 22 December 2016
This paper describes the three-dimensional destabilization characteristics of an annular liquid sheet when subjected to the combined action of Rayleigh–Taylor (RT) and Kelvin–Helmholtz (KH) instability mechanisms. The stability characteristics are studied using temporal linear stability analysis and by assuming that the fluids are incompressible, immiscible and inviscid. Surface tension is also taken into account at both the interfaces. Linearized equations governing the growth of instability amplitude have been derived. These equations involve time-varying coefficients and have been analysed using two approaches – direct numerical time integration and frozen-flow approximation. From the direct numerical time integration, we show that the time-varying coefficients evolve on a slow time scale in comparison with the amplitude growth. Therefore, we justify the use of the frozen-flow approximation and derive a closed-form dispersion relation from the appropriate governing equations and boundary conditions. The effect of flow conditions and fluid properties is investigated by introducing dimensionless numbers such as Bond number (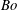 $Bo$), inner and outer Weber numbers (
$Bo$), inner and outer Weber numbers (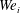 $We_{i}$,
$We_{i}$, 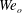 $We_{o}$) and inner and outer density ratios (
$We_{o}$) and inner and outer density ratios (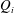 $Q_{i}$,
$Q_{i}$, 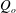 $Q_{o}$). We show that four instability modes are possible – Taylor, sinuous, flute and helical. It is observed that the choice of instability mode is influenced by a combination of both
$Q_{o}$). We show that four instability modes are possible – Taylor, sinuous, flute and helical. It is observed that the choice of instability mode is influenced by a combination of both 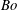 $Bo$ as well as
$Bo$ as well as 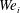 $We_{i}$ and
$We_{i}$ and 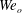 $We_{o}$. However, the instability length scale calculated from the most unstable wavenumbers is primarily a function of
$We_{o}$. However, the instability length scale calculated from the most unstable wavenumbers is primarily a function of 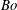 $Bo$. We show a regime map in the
$Bo$. We show a regime map in the 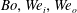 $Bo,We_{i},We_{o}$ parameter space to identify regions where the system is susceptible to three-dimensional helical modes. Finally, we show an optimal partitioning of a given total energy (
$Bo,We_{i},We_{o}$ parameter space to identify regions where the system is susceptible to three-dimensional helical modes. Finally, we show an optimal partitioning of a given total energy (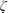 $\unicode[STIX]{x1D701}$) into acceleration-induced and shear-induced instability mechanisms in order to achieve a minimum instability length scale (
$\unicode[STIX]{x1D701}$) into acceleration-induced and shear-induced instability mechanisms in order to achieve a minimum instability length scale (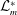 ${\mathcal{L}}_{m}^{\ast }$). We show that it is beneficial to introduce at least 90 % of the total energy into acceleration induced RT instability mechanism. In addition, we show that when the RT mechanism is invoked to destabilize an annular liquid sheet,
${\mathcal{L}}_{m}^{\ast }$). We show that it is beneficial to introduce at least 90 % of the total energy into acceleration induced RT instability mechanism. In addition, we show that when the RT mechanism is invoked to destabilize an annular liquid sheet, 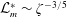 ${\mathcal{L}}_{m}^{\ast }\sim \unicode[STIX]{x1D701}^{-3/5}$.
${\mathcal{L}}_{m}^{\ast }\sim \unicode[STIX]{x1D701}^{-3/5}$.