Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T03:10:41.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Contact lines with a 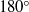$18{0}^{\circ } $ contact angle

Published online by Cambridge University Press:  08 February 2013

E. S. Benilov  and
M. Vynnycky
E. S. Benilov*
Affiliation:
Mathematics Applications Consortium for Science and Industry, Department of Mathematics and Statistics, University of Limerick, Limerick, Ireland
M. Vynnycky
Affiliation:
Mathematics Applications Consortium for Science and Industry, Department of Mathematics and Statistics, University of Limerick, Limerick, Ireland
*
†Email address for correspondence: Eugene.Benilov@ul.ie
Get access Rights & Permissions [Opens in a new window]

Abstract

This work builds on the foundation laid by Benney & Timson (Stud. Appl. Maths, vol. 63, 1980, pp. 93–98), who examined the flow near a contact line and showed that, if the contact angle is 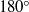$18{0}^{\circ } $, the usual contact-line singularity does not arise. Their local analysis, however, does not allow one to determine the velocity of the contact line and their expression for the shape of the free boundary involves undetermined constants. The present paper considers two-dimensional Couette flows with a free boundary, for which the local analysis of Benney & Timson can be complemented by an analysis of the global flow (provided that the slope of the free boundary is small, so the lubrication approximation can be used). We show that the undetermined constants in the solution of Benney & Timson can all be fixed by matching the local and global solutions. The latter also determines the contact line’s velocity, which we compute among other characteristics of the global flow. The asymptotic model derived is used to examine steady and evolving Couette flows with a free boundary. It is shown that the latter involve brief intermittent periods of rapid acceleration of contact lines.

JFM classification

Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Lubrication theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 718 , 10 March 2013 , pp. 481 - 506
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aussillous, P. & Quéré, D. 2004 Shapes of rolling liquid drops. J. Fluid Mech. 512, 133–151.Google Scholar
Benilov, E. S. 2004 Explosive instability in a linear system with neutrally stable eigenmodes. Part 2: multi-dimensional disturbances. J. Fluid Mech. 501, 105–124.CrossRefGoogle Scholar
Benilov, E. S., Chapman, S. J., Mcleod, J. B., Ockendon, J. R. & Zubkov, V. S. 2010 On liquid films on an inclined plate. J. Fluid Mech. 663, 53–69.CrossRefGoogle Scholar
Benilov, E. S., O’Brien, S. B. G. & Sazonov, I. A. 2003 A new type of instability: explosive disturbances in a liquid film inside a rotating horizontal cylinder. J. Fluid Mech. 497, 201–224.Google Scholar
Benney, D. J. & Timson, W. J. 1980 The rolling motion of a viscous fluid on and off a rigid surface. Stud. Appl. Maths 63, 93–98.Google Scholar
Bertozzi, A. L. & Pugh, M. 1996 The lubrication approximation for thin viscous films: regularity and long-time behaviour of weak solutions. Commun. Pure Appl. Maths 49, 85–123.Google Scholar
Bertozzi, A. L. & Pugh, M. 2000 Finite-time blow-up of solutions of some long-wave unstable thin film equations. Indiana Univ. Math. J. 49, 1323–1366.Google Scholar
Biance, A.-L., Clanet, C. & Quéré, D. 2003 Leidenfrost drops. Phys. Fluids 15, 1632–1637.CrossRefGoogle Scholar
Biance, A.-L., Pirat, C. & Ybert, C. 2011 Drop fragmentation due to hole formation during Leidenfrost impact. Phys. Fluids 23, 022104.Google Scholar
Didenkulova, I., Pelinovsky, E., Soomere, T. & Zahibo, N. 2007 Runup of nonlinear asymmetric waves on a plane beach. In Tsunami and Nonlinear Waves (ed. Kundu, A.). pp. 175–190. Springer.CrossRefGoogle Scholar
Dussan V., E. B. 1976 The moving contact line: the slip boundary condition. J. Fluid Mech. 77, 665–684.Google Scholar
Dussan V., E. B. & Davis, S. H. 1974 On the motion of a fluid–fluid interface along a solid surface. J. Fluid Mech. 65, 71–95.Google Scholar
Fujima, K. 2007 Tsunami runup in Lagrangian description. In Tsunami and Nonlinear Waves (ed. Kundu, A.). pp. 191–208. Springer.Google Scholar
Hervet, H. & de Gennes, P.-G. 1984 The dynamics of wetting: precursor films in the wetting of ‘dry’ solids. C. R. Acad. Sci., Ser. II: Mec., Phys., Chim., Sci. Terre Univers 299, 499–503.Google Scholar
Hocking, L. M. 1976 A moving fluid interface on a rough surface. J. Fluid Mech. 76, 801–817.CrossRefGoogle Scholar
Hocking, L. M. 1977 A moving fluid interface. Part 2. The removal of the force singularity by a slip flow. J. Fluid Mech. 79, 209–229.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101.Google Scholar
Landau, L. & Levich, B. 1942 Dragging of liquid by a plate. Acta Physiochim. USSR 17, 42–54.Google Scholar
Lauga, E. & Brenner, M. P. 2004 Dynamic mechanisms for apparent slip on hydrophobic surfaces. Phys. Rev. E 70, 026311, 7 pages.Google Scholar
Mahadevan, L. & Pomeau, Y. 1999 Rolling droplets. Phys. Fluids 11, 2449–2453.Google Scholar
Madsen, P. A. & Fuhrman, D. R. 2007 Analytical and numerical models for tsunami run-up. In Tsunami and Nonlinear Waves (ed. Kundu, A.). pp. 209–236. Springer.Google Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.Google Scholar
Ngan, C. G. & Dussan V., E. B. 1984 The moving contact line with a $18{0}^{\circ } $ advancing contact angle. Phys. Fluids 24, 2785–2787.CrossRefGoogle Scholar
Pismen, L. M. & Nir, A. 1982 Motion of a contact line. Phys. Fluids 25, 3–7.CrossRefGoogle Scholar
Reznik, S. N. & Yarin, A. L. 2002 Spreading of a viscous drop due to gravity and capillarity on a horizontal or an inclined dry wall. Phys. Fluids 14, 911–925.CrossRefGoogle Scholar
Richard, D. & Quéré, D. 1999 Viscous drops rolling on a tilted non-wettable solid. Europhys. Lett. 48, 286–291.Google Scholar
Seppecher, P. 1996 Moving contact lines in the Cahn-Hilliard theory. Intl J. Engng Sci. 34, 977–992.Google Scholar
Shikhmurzaev, Yu. D. 1993 The moving contact line on a smooth solid surface. Intl J. Multiphase Flow 19, 589–610.Google Scholar
Talanov, V. I. 1964 Self-focusing of electromagnetic waves in nonlinear media. Radiophys. 8, 254–257.Google Scholar
Thompson, P. A. & Troian, S. M. 1997 A general boundary condition for liquid flow at solid surfaces. Nature 389, 360–362.Google Scholar
Wayner, P. C. 1993 Spreading of a liquid film with a finite contact angle by the evapouration/condensation process. Langmuir 9, 294–299.Google Scholar
Weidner, D. E. & Schwartz, L. W. 1994 Contact-line motion of shear-thinning liquids. Phys. Fluids 6, 3535–3538.Google Scholar
Wilson, S. D. R. 1982 The drag-out problem in film coating theory. J. Engng Maths 16, 209–221.Google Scholar
Zakharov, V. E. 1972 Collapse of Langmuir waves. Sov. Phys. JETP 35, 908–914.Google Scholar