Article contents
Controlled stabilization of rotating toroidal drops in viscous linear flow
Published online by Cambridge University Press: 01 December 2022
Abstract
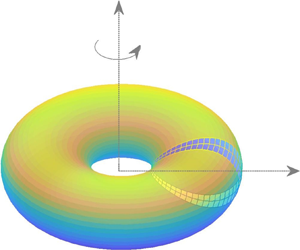
Toroidal drops, embedded in viscous flow, have a large range of stationary shapes that are challenging to compute numerically due to their inherent instability. When both the drop and the outer fluid are Newtonian liquids, the only reported cases of such stable configurations are of highly expanded drops rotating in an axisymmetrical extensional flow. In this study, we propose a method for stabilizing the stationary shapes of inherently unstable rotating toroidal drops, embedded in extensional or biextensional flow, by subjecting the system to feedback control stabilization. The proposed controller is designed using a two-state dynamic model of the system and is tested on a high-order nonlinear dynamic model of the drop deformation. It is demonstrated that, through this simplified feedback-control-centred approach, an extended collection of stabilized stationary solutions is generated, which spans the range from highly expanded drops to almost collapsed ones. In the latter region, that was never obtained in previous studies, multiplicity of solutions is identified. Furthermore, our method is more accurate and more efficient compared with the previously used ones.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 1
- Cited by


