Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T12:09:21.382Z Has data issue: false hasContentIssue false
  • English
  • Français

Convection in a rapidly rotating cylindrical annulus with laterally varying boundary heat flux

Published online by Cambridge University Press:  19 November 2019

Swarandeep Sahoo  and
Binod Sreenivasan Open the ORCID record for Binod Sreenivasan [Opens in a new window]
Swarandeep Sahoo
Affiliation:
Centre for Earth Sciences, Indian Institute of Science, Bangalore560012, India
Binod Sreenivasan*
Affiliation:
Centre for Earth Sciences, Indian Institute of Science, Bangalore560012, India
*
†Email address for correspondence: bsreeni@iisc.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Convection in a rapidly rotating cylindrical annulus subject to azimuthal variations in outer boundary heat flux is investigated experimentally. The motivation for this problem stems from the influence of the laterally inhomogeneous lower mantle on the geodynamo. The absence of axial ($z$) gradients of boundary temperature ensures that the condition of quasi-geostrophy, often used to model convection outside the tangent cylinder in spherical shells, is realized in a cylindrical annulus even in strongly driven convection. Experiments are performed with water from below onset of convection to highly supercritical states (measured by the flux Rayleigh number, $Ra\sim 10^{10}$) and for boundary heat flux heterogeneity $q^{\ast }$ (defined by the ratio of the azimuthal variation to the mean boundary heat flux) in the range 0–2. 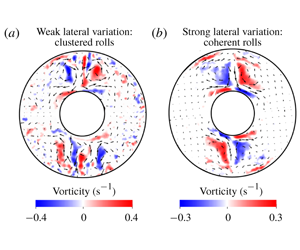The power requirement for onset of convection reduces substantially with increasing $q^{\ast }$, in line with earlier studies of the onset in rotating spherical shells. For strongly driven convection at $q^{\ast }>1$, the long-time structure is that of localized coherent cyclone–anticyclone vortex pairs, which produce narrow downwellings between them. However, shorter-time averages of the flow reveal the presence of small-scale motions, which may have an important role in magnetic field generation. For a twofold heat flux heterogeneity of $q^{\ast }\approx 2$, convection within the annulus fully homogenizes at ${\sim}30$ times the onset Rayleigh number, and no coherent vortices remain. Finally, the measured heat flux variation on the inner boundary is considerably larger compared with that on the outer boundary, which provides a plausible mechanism for inner-core heterogeneity in the Earth.

JFM classification

Geophysical and Geological Flows: Geodynamo Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A1
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Brown, E., Araujo, F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
Alonso, A., Net, M., Mercader, I. & Knobloch, E. 1999 Onset of convection in a rotating annulus with radial gravity and heating. Fluid Dyn. Res. 24 (3), 133–145.CrossRefGoogle Scholar
Amit, H. & Choblet, G. 2009 Mantle-driven geodynamo features – effects of post-Perovskite phase transition. Earth Planet. Space 61 (11), 1255–1268.CrossRefGoogle Scholar
Anufriev, A. P., Jones, C. A. & Soward, A. M. 2005 The Boussinesq and anelastic liquid approximations for convection in the Earth’s core. Phys. Earth Planet. Inter. 152, 163–190.CrossRefGoogle Scholar
Aubert, J., Amit, H., Hulot, G. & Olson, P. 2008 Thermo-chemical wind flows couple Earth’s inner core growth to mantle heterogeneity. Nature 454, 758–761.CrossRefGoogle Scholar
Aubert, J., Finlay, C. C. & Fournier, A. 2013 Bottom-up control of geomagnetic secular variation by the Earth’s inner core. Nature 502, 219–223.CrossRefGoogle ScholarPubMed
Azouni, M. A., Bolton, E. W. & Busse, F. H. 1985 Convection driven by centrifugal bouyancy in a rotating annulus. Geophys. Astrophys. Fluid Dyn. 34 (1-4), 301–317.CrossRefGoogle Scholar
Bergman, M. I. 1997 Measurements of electric anisotropy due to solidification texturing and the implications for the Earth’s inner core. Nature 389 (6646), 60–63.CrossRefGoogle Scholar
Bloxham, J. & Gubbins, D. 1987 Thermal core-mantle interactions. Nature 325, 511–513.CrossRefGoogle Scholar
Boisson, J., Cébron, D., Moisy, F. & Cortet, P. P. 2012 Earth rotation prevents exact solid-body rotation of fluids in the laboratory. Eur. Phys. Lett. 98 (5), 59002.Google Scholar
Bréger, L. & Romanowicz, B. 1998 Three-dimensional structure at the base of the mantle beneath the central pacific. Science 282 (5389), 718–720.Google ScholarPubMed
Busse, F. H. 1986 Asymptotic theory of convection in a rotating, cylindrical annulus. J. Fluid Mech. 173, 545–556.CrossRefGoogle Scholar
Busse, F. H. & Carrigan, C. R. 1976 Laboratory simulation of thermal convection in rotating planets and stars. Science 191, 81–83.CrossRefGoogle ScholarPubMed
Calkins, M., Hale, K., Julien, K., Nieves, D., Driggs, D. & Marti, P. 2015 The asymptotic equivalence of fixed heat flux and fixed temperature thermal boundary conditions for rapidly rotating convection. J. Fluid Mech. 784, R2.CrossRefGoogle Scholar
Calkins, M. A. 2018 Quasi-geostrophic dynamo theory. Phys. Earth Planet. Inter. 276, 182–189.CrossRefGoogle Scholar
Carrigan, C. R. & Busse, F. H. 1983 An experimental and theoretical investigation of the onset of convection in rotating spherical shells. J. Fluid Mech. 126, 287–305.CrossRefGoogle Scholar
Cordero, S. & Busse, F. H. 1992 Experiments on convection in rotating hemispherical shells: transition to a quasi-periodic state. Geophys. Res. Lett. 19 (8), 733–736.CrossRefGoogle Scholar
Cox, A. & Doell, R. R. 1964 Long period variations of the geomagnetic field. Bull. Seismol. Soc. Am. 54 (6B), 2243–2270.Google Scholar
Davies, C. J., Gubbins, D. & Jimack, P. K. 2009 Convection in a rapidly rotating spherical shell with an imposed laterally varying thermal boundary condition. J. Fluid Mech. 641, 335–358.CrossRefGoogle Scholar
Dietrich, W., Hori, K. & Wicht, J. 2016 Core flows and heat transfer induced by inhomogeneous cooling with sub- and supercritical convection. Phys. Earth Planet. Inter. 251, 36–51.CrossRefGoogle Scholar
Favier, B., Guervilly, C. & Knobloch, E. 2019 Subcritical turbulent condensate in rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 864, R1.CrossRefGoogle Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 Nek5000 Web page. Available at: http://nek5000.mcs.anl.gov.Google Scholar
Gastine, T. 2019 pizza: an open-source pseudo-spectral code for spherical quasi-geostrophic convection. Geophys. J. Intl 217 (3), 1558–1576.CrossRefGoogle Scholar
Gillet, N. & Jones, C. A. 2006 The quasi-geostrophic model for rapidly rotating spherical convection outside the tangent cylinder. J. Fluid Mech. 554, 343–369.CrossRefGoogle Scholar
Gubbins, D., Sreenivasan, B., Mound, J. & Rost, S. 2011 Melting of the Earth’s inner core. Nature 473, 361–363.CrossRefGoogle ScholarPubMed
Gubbins, D., Willis, P. W. & Sreenivasan, B. 2007 Correlation of Earth’s magnetic field with lower mantle thermal and seismic structure. Phys. Earth Planet. Inter. 162, 256–260.CrossRefGoogle Scholar
Guervilly, C. & Hughes, D. W. 2017 Jets and large-scale vortices in rotating Rayleigh–Bénard convection. Phys. Rev. Fluids 2 (11), 113503.CrossRefGoogle Scholar
Hide, R. 1958 An experimental study of thermal convection in a rotating liquid. Phil. Trans. R. Soc. Lond. A 250, 441–478.CrossRefGoogle Scholar
Hirose, K., Labrosse, S. & Hernlund, J. 2013 Compositional state of Earth’s core. Annu. Rev. Earth Planet. Sci. 41, 657–691.CrossRefGoogle Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26 (5), 055111.CrossRefGoogle Scholar
Jackson, A., Jonkers, A. R. T. & Walker, M. R. 2000 Four centuries of geomagnetic secular variation from historical records. Phil. Trans. R. Soc. Lond. A 358, 957–990.CrossRefGoogle Scholar
Jones, G. M. 1977 Thermal interaction of the core and the mantle and long-term behavior of the geomagnetic field. J. Geophys. Res. 82 (11), 1703–1709.CrossRefGoogle Scholar
Julien, K., Knobloch, E. & Plumley, M. 2018 Impact of domain anisotropy on the inverse cascade in geostrophic turbulent convection. J. Fluid Mech. 837, R4.CrossRefGoogle Scholar
King, M. P. & Wilson, M. 2005 Numerical simulations of convective heat transfer in Rayleigh–Bénard convection and a rotating annulus. Numer. Heat Transfer A 48 (6), 529–545.CrossRefGoogle Scholar
Labrosse, S. 2002 Hotspots, mantle plumes and core heat loss. Earth Planet. Sci. Lett. 199 (1-2), 147–156.CrossRefGoogle Scholar
Masters, G., Laske, G., Bolton, H. & Dziewonski, A. 2000 The relative behavior of shear velocity, bulk sound velocity, and compressional velocity in the mantle: implications for chemical and thermal structure. In Earth’s Deep Interior (ed. Karato, S., Forte, A. M., Liebermann, R. C., Masters, G. & Stixrude, L.), vol. 117. AGU monograph.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Morelli, A., Dziewonski, A. M. & Woodhouse, J. H. 1986 Anisotropy of the inner core inferred from PKIKP travel times. Geophys. Res. Lett. 13 (13), 1545–1548.CrossRefGoogle Scholar
Mound, J. E. & Davies, C. J. 2017 Heat transfer in rapidly rotating convection with heterogeneous thermal boundary conditions. J. Fluid Mech. 828, 601–629.CrossRefGoogle Scholar
Nakagawa, T. & Tackley, P. J. 2008 Lateral variations in CMB heat flux and deep mantle seismic velocity caused by a thermal-chemical-phase boundary layer in 3D spherical convection. Earth Planet. Sci. Lett. 271, 348–358.CrossRefGoogle Scholar
Offermans, N., Marin, O., Schanen, M., Gong, J., Fischer, P., Schlatter, P., Obabko, A., Peplinski, A., Hutchinson, M. & Merzari, E. 2016 On the strong scaling of the spectral element solver Nek5000 on Petascale Systems. In Proceedings of the Exascale Applications and Software Conference, doi:10.1145/2938615.2938617. ACM.Google Scholar
Olson, P. & Christensen, U. 2002 The time averaged magnetic field in numerical dynamos with nonuniform boundary heat flow. Geophys. J. Intl 151, 809–823.CrossRefGoogle Scholar
Olson, P., Deguen, R., Rudolph, M. L. & Zhong, S. 2015 Core evolution driven by mantle global circulation. Phys. Earth Planet. Inter. 243, 44–55.CrossRefGoogle Scholar
Olson, P., Landeau, M. & Reynolds, E. 2017 Dynamo tests for stratification below the core–mantle boundary. Phys. Earth Planet. Inter. 271, 1–18.CrossRefGoogle Scholar
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. 2012 Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485, 355–358.CrossRefGoogle ScholarPubMed
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. 2013 Transport properties for liquid silicon-oxygen-iron mixtures at Earth’s core conditions. Phys. Rev. B 87, 014110.CrossRefGoogle Scholar
Ritsema, J., van Heijst, H. J. & Woodhouse, J. H. 1999 Complex shear wave velocity structure imaged beneath Africa and Iceland. Science 286 (5446), 1925–1928.CrossRefGoogle Scholar
Sahoo, S. & Sreenivasan, B. 2017 On the effect of laterally varying boundary heat flux on rapidly rotating spherical shell convection. Phys. Fluids 29 (8), 086602.CrossRefGoogle Scholar
Sahoo, S., Sreenivasan, B. & Amit, H. 2016 Dynamos driven by weak thermal convection and heterogeneous outer boundary heat flux. Phys. Earth Planet. Inter. 250, 35–45.CrossRefGoogle Scholar
Sreenivasan, B. 2009 On dynamo action produced by boundary thermal coupling. Phys. Earth Planet. Inter. 177, 130–138.CrossRefGoogle Scholar
Sreenivasan, B. & Gopinath, V. 2017 Confinement of rotating convection by a laterally varying magnetic field. J. Fluid Mech. 822, 590–616.CrossRefGoogle Scholar
Sreenivasan, B. & Gubbins, D. 2008 Dynamos with weakly convecting outer layers: implications for core–mantle boundary interaction. Geophys. Astrophys. Fluid Dyn. 102, 395–407.CrossRefGoogle Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.CrossRefGoogle Scholar
Sumita, I. & Olson, P. 1999 A laboratory model for convection in Earth’s core driven by a thermally heterogeneous mantle. Science 286 (5444), 1547–1549.CrossRefGoogle ScholarPubMed
Sumita, I. & Olson, P. 2002 Rotating thermal convection experiments in a hemispherical shell with heterogeneous boundary heat flux: implications for the Earth’s core. J. Geophys. Res. Solid Earth 107 (B8), 2169.CrossRefGoogle Scholar
Sun, Z.-P., Schubert, G. & Glatzmaier, G. A. 1994 Numerical simulations of thermal convection in a rapidly rotating spherical shell cooled inhomogeneously from above. Geophys. Astrophys. Fluid Dyn. 75, 199–226.CrossRefGoogle Scholar
Takahashi, F., Tsunakawa, H., Matsushima, M., Mochizuki, N. & Honkura, Y. 2008 Effects of thermally heterogeneous structure in the lowermost mantle on the geomagnetic field strength. Earth Planet. Sci. Lett. 272 (3-4), 738–746.CrossRefGoogle Scholar
Tanaka, S. & Hamaguchi, H. 1997 Degree one heterogeneity and hemispherical variation of anisotropy in the inner core from PKP(BC)–PKP(DF) times. J. Geophys Res. Solid Earth 102 (B2), 2925–2938.CrossRefGoogle Scholar
Thielicke, W. & Stamhuis, E. 2014 PIVlab – towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Research Software 2 (1), e30.CrossRefGoogle Scholar
Williams, Q., Revenaugh, J. & Garnero, E. 1998 A correlation between ultra-low basal velocities in the mantle and hot spots. Science 281 (5376), 546–549.CrossRefGoogle ScholarPubMed
Willis, P. W., Sreenivasan, B. & Gubbins, D. 2007 Thermal core-mantle interaction: exploring regimes for ‘locked’ dynamo action. Phys. Earth Planet. Inter. 165, 83–92.CrossRefGoogle Scholar
Yuen, D. A., Cadek, O., Chopelas, A. & Matyska, C. 1993 Geophysical inferences of thermal-chemical structures in the lower mantle. Geophys. Res. Lett. 20 (10), 899–902.CrossRefGoogle Scholar
Zhang, K. & Greed, G. T. 1998 Convection in rotating annulus: an asymptotic theory and numerical solutions. Phys. Fluids 10 (9), 2396.CrossRefGoogle Scholar
Zhang, K. & Gubbins, D. 1993 Convection in a rotating spherical fluid shell with an inhomogeneous temperature boundary condition at infinite Prandtl number. J. Fluid Mech. 250, 209–232.CrossRefGoogle Scholar