Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T06:53:07.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Convective carbon dioxide dissolution in a closed porous medium at low pressure

Published online by Cambridge University Press:  31 August 2018

Baole Wen Open the ORCID record for Baole Wen [Opens in a new window] ,
Daria Akhbari ,
Li Zhang Open the ORCID record for Li Zhang [Opens in a new window]  and
Marc A. Hesse
Baole Wen
Affiliation:
Institute for Computational Engineering and Sciences, University of Texas at Austin, Austin, TX 78712, USA
Daria Akhbari
Affiliation:
Department of Geological Sciences, University of Texas at Austin, Austin, TX 78712, USA
Li Zhang
Affiliation:
Department of Engineering Mechanics, Tsinghua University, Beijing, 100084, China
Marc A. Hesse*
Affiliation:
Institute for Computational Engineering and Sciences, University of Texas at Austin, Austin, TX 78712, USA Department of Geological Sciences, University of Texas at Austin, Austin, TX 78712, USA
*
†Email address for correspondence: mhesse@jsg.utexas.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

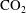Motivated by the persistence of natural carbon dioxide ($\text{CO}_{2}$) fields, we investigate the convective dissolution of 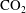$\text{CO}_{2}$ at low pressure (below 1 MPa) in a closed system, where the pressure in the gas declines as convection proceeds. This introduces a negative feedback that reduces the convective dissolution rate even before the brine becomes saturated. We analyse the case of an ideal gas with a solubility given by Henry’s law, in the limits of very low and very high Rayleigh numbers. The equilibrium state in this system is determined by the dimensionless dissolution capacity, 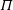$\unicode[STIX]{x1D6F1}$, which gives the fraction of the gas that can be dissolved into the underlying brine. Analytic approximations of the pure diffusion problem with 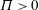$\unicode[STIX]{x1D6F1}>0$ show that the diffusive base state is no longer self-similar and that diffusive mass transfer declines rapidly with time. Direct numerical simulations at high Rayleigh numbers show that no constant flux regime exists for 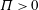$\unicode[STIX]{x1D6F1}>0$; nevertheless, the quantity 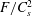$F/C_{s}^{2}$ remains constant, where 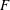$F$ is the dissolution flux and 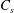$C_{s}$ is the dissolved concentration at the top of the domain. Simple mathematical models are developed to predict the evolution of 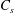$C_{s}$ and 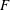$F$ for high-Rayleigh-number convection in a closed system. The negative feedback that limits convection in closed systems may explain the persistence of natural 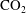$\text{CO}_{2}$ accumulations over millennial time scales.

JFM classification

Convection: Convection Convection: Convection in porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , pp. 56 - 87
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhbari, D. & Hesse, M. A. 2017 Causes of underpressure in natural CO2 reservoirs and implications for geological storage. Geology 45, 47–50.Google Scholar
Azin, R., Mahmoudy, M., Raad, S. M. J. & Osfouri, S. 2013 Measurement and modeling of CO2 diffusion coefficient in saline aquifer at reservoir conditions. Cent. Eur. J. Engng 3, 585–594.Google Scholar
Backhaus, S., Turitsyn, K. & Ecke, R. E. 2011 Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 106, 104501.Google Scholar
Barletta, A. & Storesletten, L. 2012 Onset of convection in a porous rectangular channel with external heat transfer to upper and lower fluid environments. Trans. Porous Med. 94, 659–681.Google Scholar
Barletta, A., Tyvand, P. A. & Nygøard, H. S. 2015 Onset of thermal convection in a porous layer with mixed boundary conditions. J. Engng Maths 91, 105–120.Google Scholar
Bickle, M., Chadwick, A., Huppert, H. E., Hallworth, M. & Lyle, S. 2007 Modelling carbon dioxide accumulation at Sleipner: implications for underground carbon storage. Earth Planet. Sci. Lett. 255, 164–176.Google Scholar
Boyd, J. P. 2000 Chebyshev and Fourier Spectral Methods, 2nd edn. Dover.Google Scholar
Broadhead, R. F. 1987 Carbon dioxide in Union and Harding counties. In New Mexico Geological Society Guidebook, 38th Field Conference, pp. 339–349. New Mexico Geological Society.Google Scholar
Broadhead, R. F. 1990 Structural Traps I: Tectonic Fold Traps. American Association of Petroleum Geologists.Google Scholar
Crank, J. 1975 The Mathematics of Diffusion, 2nd edn. Oxford University Press.Google Scholar
Doering, C. R. & Constantin, P. 1998 Bounds for heat transport in a porous layer. J. Fluid Mech. 376, 263–296.Google Scholar
Duan, Z. & Sun, R. 2003 An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 193, 257–271.Google Scholar
Duffy, D. G. 2004 Transform Methods for Solving Partial Differential Equations, 2nd edn. Chapman & Hall/CRC.Google Scholar
Efika, E. C., Hoballah, R., Li, X., May, E. F., Nania, M., Sanchez-Vicente, Y. & Trusler, J. P. M. 2016 Saturated phase densities of (CO2 + H2O) at temperatures from (293 to 450) K and pressures up to 64 MPa. J. Chem. Thermodyn. 93, 347–359.Google Scholar
Elenius, M. T. & Johannsen, K. 2012 On the time scales of nonlinear instability in miscible displacement porous media flow. Comput. Geosci. 16, 901–911.Google Scholar
Elenius, M. T., Nordbotten, J. M. & Kalisch, H. 2014 Convective mixing influenced by the capillary transition zone. Comput. Geosci. 18, 417–431.Google Scholar
Emami-Meybodi, H., Hassanzadeh, H., Green, C. P. & Ennis-King, J. 2015 Convective dissolution of CO2 in saline aquifers: progress in modeling and experiments. Intl J. Greenh. Gas Control 40, 238–266.Google Scholar
Ennis-King, J., Preston, I. & Paterson, L. 2005 Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, 084107.Google Scholar
Farajzadeh, R., Zitha, P. L. J. & Bruining, J. 2007 Mass transfer of CO2 into water and surfactant solutions. Petrol. Sci. Technol. 25, 1493–1511.Google Scholar
Farajzadeh, R., Zitha, P. L. J. & Bruining, J. 2009 Enhanced mass transfer of CO2 into water: Experiment and modeling. Ind. Engng Chem. Res. 48, 6423–6431.Google Scholar
Fu, X., Cueto-Felgueroso, L. & Juanes, R. 2013 Pattern formation and coarsening dynamics in three-dimensional convective mixing in porous media. Phil. Trans. R. Soc. Lond. A 371, 20120355.Google Scholar
Gilfillan, S. M. V., Ballentine, C. J., Holland, G., Blagburn, D., Lollar, B. S., Stevens, S., Schoell, M. & Cassidy, M. 2008 The noble gas geochemistry of natural CO2 gas reservoirs from the Colorado Plateau and Rocky Mountain provinces, USA. Geochim. Cosmochim. Acta 72, 1174–1198.Google Scholar
Gilfillan, S. M. V., Lollar, B. S., Holland, G., Blagburn, D., Stevens, S., Schoell, M., Cassidy, M., Ding, Z., Zhou, Z., Lacrampe-Couloume, G. & Ballentine, C. J. 2009 Solubility trapping in formation water as dominant CO2 sink in natural gas fields. Nature 458, 614–618.Google Scholar
Gist, G. A., Thompson, A. H., Katz, A. J. & Higgins, R. L. 1990 Hydrodynamic dispersion and pore geometry in consolidated rock. Phys. Fluids A 2, 1533–1544.Google Scholar
Golding, M. J., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2011 Two-phase gravity currents in porous media. J. Fluid Mech. 678, 248–270.Google Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2006 Stability of a fluid in a horizontal saturated porous layer: effect of non-linear concentration profile, initial, and boundary conditions. Trans. Porous Med. 65, 193–211.Google Scholar
Hassanzadeh, P., Chini, G. P. & Doering, C. R. 2014 Wall to wall optimal transport. J. Fluid Mech. 751, 627–662.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2014 High Rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 748, 879–895.Google Scholar
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109, 264503.Google Scholar
Hitchen, J. & Wells, A. J. 2016 The impact of imperfect heat transfer on the convective instability of a thermal boundary layer in a porous media. J. Fluid Mech. 794, 154–174.Google Scholar
Horton, C. W. & Rogers, F. T. 1945 Convection currents in a porous medium. J. Appl. Phys. 16, 367–370.Google Scholar
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272.Google Scholar
Hürlimann, M. D., Helmer, K. G., Latour, L. L. & Sotak, C. H. 1994 Restricted diffusion in sedimentary rocks: determination of surface-area-to-volume ratio and surface relaxivity. J. Magn. Reson A 111, 169–178.Google Scholar
Jacob, R. & Saylor, B. Z. 2016 CO2 solubility in multi-component brines containing NaCl, KCl, CaCl2 and MgCl2 at 297 K and 1–14 MPa. Chem. Geol. 424, 86–95.Google Scholar
Javaheri, M., Abedi, J. & Hassanzadeh, H. 2010 Linear stability analysis of double-diffusive convection in porous media, with application to geological storage of CO2 . Trans. Porous Med. 84, 441–456.Google Scholar
Kim, M. C. 2015 The effect of boundary conditions on the onset of buoyancy-driven convection in a brine-saturated porous medium. Trans. Porous Med. 107, 469–487.Google Scholar
Kim, M. C. & Choi, C. K. 2012 Linear stability analysis on the onset of buoyancy-driven convection in liquid-saturated porous medium. Phys. Fluids 24, 044102.Google Scholar
Kim, M. C., Song, K. H., Choi, C. K. & Yeo, J.-K. 2008 Onset of buoyancy-driven convection in a liquid-saturated cylindrical porous layer supported by a gas layer. Phys. Fluids 20, 054104.Google Scholar
Kim, M. C., Yoon, D. Y. & Choi, C. K. 2006 Onset of buoyancy-driven instability in gas diffusion systems. Ind. Engng Chem. Res. 45, 7321–7328.Google Scholar
Kubitschek, J. P. & Weidman, P. D. 2003 Stability of a fluid-saturated porous medium heated from below by forced convection. Intl J. Heat Mass Transfer 46, 3697–3705.Google Scholar
Lapwood, E. R. 1948 Convection of a fluid in a porous medium. Proc. Camb. Phil. Soc. 44, 508–521.Google Scholar
Ma, X., Abe, Y., Kaneko, A., Fujimoto, S. & Murakami, C. 2017 Study on dissolution process of liquid CO2 into water under high pressure condition for CCS. Energy Procedia 114, 5430–5437.Google Scholar
Mao, S., Zhang, D., Li, Y. & Liu, N. 2013 An improved model for calculating CO2 solubility in aqueous NaCl solutions and the application to CO2 –H2O–NaCl fluid inclusions. Chem. Geol. 347, 43–58.Google Scholar
Martinez, M. J. & Hesse, M. A. 2016 Two-phase convective CO2 dissolution in saline aquifers. Water Resour. Res. 52, 585–599.Google Scholar
Metz, B., Davidson, O., de Coninck, H., Loos, M. & Meyer, L. 2005 IPCC Special Report on Carbon Dioxide Capture and Storage. Cambridge University Press.Google Scholar
Miocic, J. M., Gilfillan, S. M. V., Roberts, J. J., Edlmann, K., McDermott, C. I. & Haszeldine, R. S. 2016 Controls on CO2 storage security in natural reservoirs and implications for CO2 storage site selection. Intl J. Greenh. Gas Control 51, 118–125.Google Scholar
Moghaddam, R. N., Rostami, B., Pourafshary, P. & Fallahzadeh, Y. 2012 Quantification of density-driven natural convection for dissolution mechanism in CO2 sequestration. Trans. Porous Med. 92, 439–456.Google Scholar
Mojtaba, S., Behzad, R., Rasoul, N. M. & Mohammad, R. 2014 Experimental study of density-driven convection effects on CO2 dissolution rate in formation water for geological storage. J. Nat. Gas Sci. Engng 21, 600–607.Google Scholar
Moortgat, J. 2018 Reservoir simulation with the cubic plus (cross-) association equation of state for water, CO2 , hydrocarbons, and tracers. Adv. Water Resour 114, 29–44.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.Google Scholar
Nikitin, N. 2006 Third-order-accurate semi-implicit Runge–Kutta scheme for incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 51, 221–233.Google Scholar
Orr, F. M. 2009 Onshore geologic storage of CO2 . Science 325, 1656–1658.Google Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.Google Scholar
Paoli, M. D., Zonta, F. & Soldati, A. 2016 Influence of anisotropic permeability on convection in porous media: implications for geological CO2 sequestration. Phys. Fluids 28 (5), 056601.Google Scholar
Paoli, M. D., Zonta, F. & Soldati, A. 2017 Dissolution in anisotropic porous media: modelling convection regimes from onset to shutdown. Phys. Fluids 29, 026601.Google Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in CO2 storage in saline aquifers. Adv. Water Resour. 33, 443–455.Google Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow. Springer.Google Scholar
Raad, S. M. J., Azin, R. & Osfouri, S. 2015 Measurement of CO2 diffusivity in synthetic and saline aquifer solutions at reservoir conditions: the role of ion interactions. Heat Mass Transfer 51, 1587–1595.Google Scholar
Riaz, A. & Cinar, Y. 2014 Carbon dioxide sequestration in saline formations. Part I. Review of the modeling of solubility trapping. J. Petrol. Sci. Engng 124, 367–380.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. Jr 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Riazi, M. R. 1996 A new method for experimental measurement of diffusion coefficients in reservoir fluids. J. Petrol. Sci. Engng 14, 235–250.Google Scholar
Sathaye, K. J., Hesse, M. A., Cassidy, M. & Stockli, D. F. 2014 Constraints on the magnitude and rate of CO2 dissolution at Bravo Dome natural gas field. Proc. Natl Acad. Sci. USA 111, 15332–15337.Google Scholar
Schiff, J. L. 1999 The Laplace Transform: Theory and Applications. Springer.Google Scholar
Sheikha, H., Pooladi-Darvish, M. & Mehrotra, A. K. 2005 Development of graphical methods for estimating the diffusivity coefficient of gases in bitumen from pressure-decay data. Energy Fuels 19, 2041–2049.Google Scholar
Shi, Z., Wen, B., Hesse, M. A., Tsotsis, T. T. & Jessen, K. 2018 Measurement and modeling of CO2 mass transfer in brine at reservoir conditions. Adv. Water Resour. 113, 100–111.Google Scholar
Slim, A. C. 2014 Solutal-convection regimes in a two-dimensional porous medium. J. Fluid Mech. 741, 461–491.Google Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 25, 024101.Google Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22, 124103.Google Scholar
Szulczewski, M. L., Hesse, M. A. & Juanes, R. 2013 Carbon dioxide dissolution in structural and stratigraphic traps. J. Fluid Mech. 736, 287–315.Google Scholar
Tilton, N. & Riaz, A. 2014 Nonlinear stability of gravitationally unstable, transient, diffusive boundary layers in porous media. J. Fluid Mech. 745, 251–278.Google Scholar
Tse, F. C. & Sandall, O. C. 1979 Diffusion coefficients for oxygen and carbon dioxide in water at 25 °C by unsteady state desorption from a quiescent liquid. Chem. Engng Commun. 3, 147–153.Google Scholar
Unwin, H. J. T., Wells, G. N. & Woods, A. W. 2016 CO2 dissolution in a background hydrological flow. J. Fluid Mech. 789, 768–784.Google Scholar
Wang, L. S., Lang, Z. X. & Guo, T. M. 1996 Measurement and correlation of the diffusion coefficients of carbon dioxide in liquid hydrocarbons under elevated pressures. Fluid Phase Equilib. 117, 364–372.Google Scholar
Weir, G. J., White, S. P. & Kissling, W. M. 1995 Reservoir storage and containment of greenhouse gases. Energy Convers. Manage. 36, 531–534.Google Scholar
Wen, B. & Chini, G. P. 2018 Inclined porous medium convection at large Rayleigh number. J. Fluid Mech. 837, 670–702.Google Scholar
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R. 2013 Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A 377, 2931–2938.Google Scholar
Wen, B., Corson, L. T. & Chini, G. P. 2015 Structure and stability of steady porous medium convection at large Rayleigh number. J. Fluid Mech. 772, 197–224.Google Scholar
Wen, B., Dianati, N., Lunasin, E., Chini, G. P. & Doering, C. R. 2012 New upper bounds and reduced dynamical modeling for Rayleigh–Bénard convection in a fluid saturated porous layer. Commun. Nonlinear Sci. Numer. Simul. 17, 2191–2199.Google Scholar
Wilkes, K. E. 1995 Onset of natural convection in a horizontal porous medium with mixed thermal boundary conditions. Trans. ASME J. Heat Transfer 117, 543–547.Google Scholar
Xu, X., Chen, S. & Zhang, D. 2006 Convective stability analysis of the long-term storage of carbon dioxide in deep saline aquifers. Adv. Water Resour. 29, 397–407.Google Scholar
Zecca, M., Honari, A., Vogt, S. J., Bijeljic, B., May, E. F. & Johns, M. L. 2016 Measurements of rock core dispersivity and tortuosity for multi-phase systems. In International Symposium of the Society of Core Analysts, Snowmass, Colorado, USA, Society of Core Analysts.Google Scholar
Zhang, L, Hesse, M. A. & Wang, M. 2017 Transient solute transport with sorption in Poiseuille flow. J. Fluid Mech. 828, 733–752.Google Scholar
Zhang, Y. P., Hyndman, C. L. & Maini, B. B. 2000 Measurement of gas diffusivity in heavy oils. J. Petrol. Sci. Engng 25, 37–47.Google Scholar