Current blockage experiments: force time histories on obstacle arrays in combined steady and oscillatory motion

Abstract

This paper revisits the problem of forces on obstacle arrays in combined waves and an in-line steady current. The intended application is the design and reassessment of offshore platforms. A series of experiments are performed on planar grids moved in both steady and oscillatory motion through otherwise stationary water. Detailed comparisons are made to a wave-current–structure interaction model recently presented by Taylor, Santo & Choo (Ocean Engng, vol. 57, 2013, pp. 11–24). We present new features of the model and test these against the experimental data. For relatively small current speed (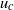${u}_{c} $) compared with oscillatory velocity amplitude (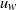${u}_{w} $) with phase angle (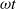$\omega t$), the drag force time history on grids with solid area (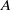$A$) and projected frontal area (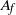${A}_{f} $) is well approximated by a summation of the wave drag and the current drag components independently, so there is no 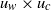${u}_{w} \times {u}_{c} $ cross-term. The wave drag component is proportional to 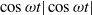$\cos \omega t\vert \cos \omega t\vert $, while the current drag component to 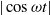$\vert \cos \omega t\vert $, i.e. it is phase-locked to the oscillatory wave crests. The form of the predicted time history is new, so much of this paper is occupied in testing the adequacy of this theoretical form both in terms of an improved Morison-type formulation and also in the precise variation of the experimental drag force in time. We show that the measured crest and trough peak values of the drag force are consistent with the force peaks and troughs of the model prediction. The odd frequency harmonics of the measured drag force scale as the square of the oscillatory velocity amplitude 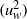$({ u}_{w}^{2} )$ and on the total hydrodynamic area (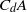${C}_{d} A$). The shape of the odd harmonics is very similar to that for a pure oscillatory motion without steady current, but there are also even frequency harmonics associated with the current component. The even harmonics of the force scale as the square of the current speed 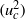$({ u}_{c}^{2} )$ and on the 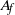${A}_{f} $, not on the 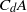${C}_{d} A$. All of the above features are identified within the experimental data, and provide considerable support for the new current blockage model.

The new model is also shown to fit the entire force time history well for a wide range of individual cases, with different blockage ratio (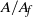$A/ {A}_{f} $) and number of grids, requiring only calibration of the Morison-type drag and inertia coefficients. In contrast, the industry-standard form of the Morison equation can only be matched at a single instant of the oscillation cycle, so present practice should be regarded as seriously inadequate for combined steady current and oscillatory flow acting on obstacle arrays.