Article contents
Detached shear-layer instability and entrainment in the wake of a flat plate with turbulent separating boundary layers
Published online by Cambridge University Press: 03 June 2015
Abstract
The near and very near wake of a flat plate with a circular trailing edge, with vigorous vortex shedding, is investigated with data from direct numerical simulations (DNS). Computations were performed for four different combinations of the Reynolds numbers based on plate thickness ( 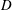 $D$ ) and momentum thickness near the trailing edge (
$D$ ) and momentum thickness near the trailing edge ( 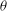 ${\it\theta}$ ). Unlike the case of the cylinder, these Reynolds numbers are independent parameters for the flat plate. The objectives of the study are twofold, to investigate the entrainment process when the separating boundary layers are turbulent and to better understand the instability of the detached shear layers (DSLs). A visualization of the entrainment process, the effect of changing the ratio
${\it\theta}$ ). Unlike the case of the cylinder, these Reynolds numbers are independent parameters for the flat plate. The objectives of the study are twofold, to investigate the entrainment process when the separating boundary layers are turbulent and to better understand the instability of the detached shear layers (DSLs). A visualization of the entrainment process, the effect of changing the ratio 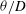 ${\it\theta}/D$ on entrainment and wake-velocity statistics, and a way of understanding entrainment in a phase-averaged sense via distributions of the turbulent transport rate are provided here. The discussion on shear-layer instability focuses on the role of log-layer eddies in the destabilization process, the effect of high-speed streaks in the turbulent boundary layer in the vicinity of the trailing edge on shear-layer vortex generation rates, and a relationship between the prevalence of shear-layer vortex generation and shedding phase that is a result of an interaction between the shedding process and the shear-layer instability mechanism. A power-law relationship between the ratio of shear-layer and shedding frequencies and the Reynolds numbers mentioned above is obtained. A discussion of the relative magnitudes of the exponents is provided. A second power-law relationship between shed-vortex strength and these two Reynolds numbers is also proposed.
${\it\theta}/D$ on entrainment and wake-velocity statistics, and a way of understanding entrainment in a phase-averaged sense via distributions of the turbulent transport rate are provided here. The discussion on shear-layer instability focuses on the role of log-layer eddies in the destabilization process, the effect of high-speed streaks in the turbulent boundary layer in the vicinity of the trailing edge on shear-layer vortex generation rates, and a relationship between the prevalence of shear-layer vortex generation and shedding phase that is a result of an interaction between the shedding process and the shear-layer instability mechanism. A power-law relationship between the ratio of shear-layer and shedding frequencies and the Reynolds numbers mentioned above is obtained. A discussion of the relative magnitudes of the exponents is provided. A second power-law relationship between shed-vortex strength and these two Reynolds numbers is also proposed.
Information
- Type
- Papers
- Information
- Copyright
- © Cambridge University Press 2015. This is a work of the U.S. Government and is not subject to copyright protection in the United States.
References
- 9
- Cited by


