Article contents
Dynamic-mode decomposition based analysis of shear coaxial jets with and without transverse acoustic driving
Published online by Cambridge University Press: 01 February 2016
Abstract
Modal decompositions of unperturbed and acoustically driven injector flows from shear coaxial jets are implemented using dynamic-mode decomposition, which is a natural approach in the search for collective oscillatory behaviour in nonlinear systems. Previous studies using proper orthogonal decomposition had revealed the most energetic pairs of coherent structures in injector flows. One of the difficulties in extracting lower-energy coherent structures follows from the need to differentiate robust flow constituents from noise and other irregular facets of a flow. The identification of robust features is critical for applications such as flow control as well, since only they can be used for the tasks. A dynamic-mode decomposition based algorithm for this differentiation is introduced and used to identify different classes of robust dynamic modes. They include (1) background modes located outside the injector flow that decay rapidly, (2) injector modes – including those presented in earlier studies – located in the vicinity of the flow, (3) modes that persist under acoustic driving, (4) modes responding linearly to the driving and, most interestingly, (5) a mode whose density exhibits antiphase oscillatory behaviour in the observation plane and that appears only when 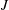 $J$ , the outer-to-inner-jet momentum flux ratio, is sufficiently large; we infer that this is a projection of a mode rotating about the symmetry axis and born via a spontaneous symmetry breaking. Each of these classes of modes is analysed as
$J$ , the outer-to-inner-jet momentum flux ratio, is sufficiently large; we infer that this is a projection of a mode rotating about the symmetry axis and born via a spontaneous symmetry breaking. Each of these classes of modes is analysed as 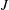 $J$ is increased, and their consequences for the flow patterns are discussed.
$J$ is increased, and their consequences for the flow patterns are discussed.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 32
- Cited by


