Article contents
Effect of mean and fluctuating pressure gradients on boundary layer turbulence
Published online by Cambridge University Press: 28 April 2014
Abstract
This study focuses on the effects of mean (favourable) and large-scale fluctuating pressure gradients on boundary layer turbulence. Two-dimensional (2D) particle image velocimetry (PIV) measurements, some of which are time-resolved, have been performed upstream of and within a sink flow for two inlet Reynolds numbers, 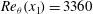 ${Re}_{\theta }(x_{1})=3360$ and 5285. The corresponding acceleration parameters,
${Re}_{\theta }(x_{1})=3360$ and 5285. The corresponding acceleration parameters, 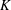 $K$ , are
$K$ , are 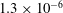 ${1.3\times 10^{-6}}$ and
${1.3\times 10^{-6}}$ and 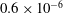 ${0.6\times 10^{-6}}$ . The time-resolved data at
${0.6\times 10^{-6}}$ . The time-resolved data at 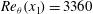 ${Re}_{\theta }(x_{1})=3360$ enables us to calculate the instantaneous pressure distributions by integrating the planar projection of the fluid material acceleration. As expected, all the locally normalized Reynolds stresses in the favourable pressure gradient (FPG) boundary layer are lower than those in the zero pressure gradient (ZPG) domain. However, the un-scaled stresses in the FPG region increase close to the wall and decay in the outer layer, indicating slow diffusion of near-wall turbulence into the outer region. Indeed, newly generated vortical structures remain confined to the near-wall region. An approximate analysis shows that this trend is caused by higher values of the streamwise and wall-normal gradients of mean streamwise velocity, combined with a slightly weaker strength of vortices in the FPG region. In both boundary layers, adverse pressure gradient fluctuations are mostly associated with sweeps, as the fluid approaching the wall decelerates. Conversely, FPG fluctuations are more likely to accompany ejections. In the ZPG boundary layer, loss of momentum near the wall during periods of strong large-scale adverse pressure gradient fluctuations and sweeps causes a phenomenon resembling local 3D flow separation. It is followed by a growing region of ejection. The flow deceleration before separation causes elevated near-wall small-scale turbulence, while high wall-normal momentum transfer occurs in the ejection region underneath the sweeps. In the FPG boundary layer, the instantaneous near-wall large-scale pressure gradient rarely becomes positive, as the pressure gradient fluctuations are weaker than the mean FPG. As a result, the separation-like phenomenon is markedly less pronounced and the sweeps do not show elevated small-scale turbulence and momentum transfer underneath them. In both boundary layers, periods of acceleration accompanying large-scale ejections involve near-wall spanwise contraction, and a high wall-normal momentum flux at all elevations. In the ZPG boundary layer, although some of the ejections are preceded, and presumably initiated, by regions of adverse pressure gradients and sweeps upstream, others are not. Conversely, in the FPG boundary layer, there is no evidence of sweeps or adverse pressure gradients immediately upstream of ejections. Apparently, the mechanisms initiating these ejections are either different from those involving large-scale sweeps or occur far upstream of the peak in FPG fluctuations.
${Re}_{\theta }(x_{1})=3360$ enables us to calculate the instantaneous pressure distributions by integrating the planar projection of the fluid material acceleration. As expected, all the locally normalized Reynolds stresses in the favourable pressure gradient (FPG) boundary layer are lower than those in the zero pressure gradient (ZPG) domain. However, the un-scaled stresses in the FPG region increase close to the wall and decay in the outer layer, indicating slow diffusion of near-wall turbulence into the outer region. Indeed, newly generated vortical structures remain confined to the near-wall region. An approximate analysis shows that this trend is caused by higher values of the streamwise and wall-normal gradients of mean streamwise velocity, combined with a slightly weaker strength of vortices in the FPG region. In both boundary layers, adverse pressure gradient fluctuations are mostly associated with sweeps, as the fluid approaching the wall decelerates. Conversely, FPG fluctuations are more likely to accompany ejections. In the ZPG boundary layer, loss of momentum near the wall during periods of strong large-scale adverse pressure gradient fluctuations and sweeps causes a phenomenon resembling local 3D flow separation. It is followed by a growing region of ejection. The flow deceleration before separation causes elevated near-wall small-scale turbulence, while high wall-normal momentum transfer occurs in the ejection region underneath the sweeps. In the FPG boundary layer, the instantaneous near-wall large-scale pressure gradient rarely becomes positive, as the pressure gradient fluctuations are weaker than the mean FPG. As a result, the separation-like phenomenon is markedly less pronounced and the sweeps do not show elevated small-scale turbulence and momentum transfer underneath them. In both boundary layers, periods of acceleration accompanying large-scale ejections involve near-wall spanwise contraction, and a high wall-normal momentum flux at all elevations. In the ZPG boundary layer, although some of the ejections are preceded, and presumably initiated, by regions of adverse pressure gradients and sweeps upstream, others are not. Conversely, in the FPG boundary layer, there is no evidence of sweeps or adverse pressure gradients immediately upstream of ejections. Apparently, the mechanisms initiating these ejections are either different from those involving large-scale sweeps or occur far upstream of the peak in FPG fluctuations.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 31
- Cited by

