Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T06:54:01.415Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of surface-charge convection on the settling velocity of spherical drops in a uniform electric field

Published online by Cambridge University Press:  24 May 2016

Ehud Yariv  and
Yaniv Almog
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
Yaniv Almog
Affiliation:
Department of Mathematics, Louisiana State University, Baton Rouge, LA 70803, USA
*
†Email address for correspondence: udi@technion.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

The mechanism of surface-charge convection, quantified by the electric Reynolds number 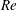$Re$, renders the Melcher–Taylor electrohydrodynamic model inherently nonlinear, with the electrostatic problem coupled to the flow. Because of this nonlinear coupling, the settling speed of a drop under a uniform electric field differs from that in its absence. This difference was calculated by Xu & Homsy (J. Fluid Mech., vol. 564, 2006, pp. 395–414) assuming small 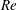$Re$. We here address the same problem using a different route, considering the case where the applied electric field is weak in the sense that the magnitude of the associated electrohydrodynamic velocity is small compared with the settling velocity. As convection is determined at leading order by the well-known flow associated with pure settling, the electrostatic problem becomes linear for arbitrary value of 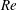$Re$. The electrohydrodynamic correction to the settling speed is then provided as a linear functional of the electric-stress distribution associated with that problem. Calculation of the settling speed eventually amounts to the solution of a difference equation governing the respective coefficients in a spherical harmonics expansion of the electric potential. It is shown that, despite the present weak-field assumption, our model reproduces the small-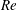$Re$ approximation of Xu and Homsy as a particular case. For finite 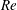$Re$, inspection of the difference equation reveals a singularity at the critical 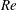$Re$-value 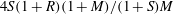$4S(1+R)(1+M)/(1+S)M$, wherein 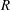$R$, 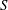$S$ and 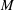$M$ respectively denote the ratios of resistivity, permittivity and viscosity values in the suspending and drop phases, as defined by Melcher & Taylor (Annu. Rev. Fluid Mech., vol. 1, 1969, pp. 111–146). Straightforward numerical solutions of this equation for electric Reynolds numbers smaller than the critical value reveal a non-monotonic dependence of the settling speed upon the electric field magnitude, including a transition from velocity enhancement to velocity decrement.

JFM classification

Drops and Bubbles: Drops and Bubbles Drops and Bubbles: Electrohydrodynamic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 797 , 25 June 2016 , pp. 536 - 548
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandopadhyay, A., Mandal, S., Kishore, N. K. & Chakraborty, S. 2016 Uniform electric-field-induced lateral migration of a sedimenting drop. J. Fluid Mech. 792, 553–589.CrossRefGoogle Scholar
Feng, J. Q. 1999 Electrohydrodynamic behaviour of a drop subjected to a steady uniform electric field at finite electric Reynolds number. Proc. R. Soc. Lond. A 455 (1986), 2245–2269.Google Scholar
Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
Jeffrey, D. J. 1996 Some basic principles in interaction calculations. In Sedimentation of Small Particles in a Viscous Fluid (ed. Torry, E. M.), chap. 4, pp. 97–124. Computational Mechanics.Google Scholar
Kim, S. & Karrila, S. J. 2005 Microhydrodynamics: Principles and Selected Applications. Dover.Google Scholar
Lanauze, J. A., Walker, L. M. & Khair, A. S. 2015 Nonlinear electrohydrodynamics of slightly deformed oblate drops. J. Fluid Mech. 774, 245–266.CrossRefGoogle Scholar
Levich, V. G. 1962 Physicochemical Hydrodynamics. Prentice-Hall.Google Scholar
Melcher, J. R. & Taylor, G. I. 1969 Electrohydrodynamics: a review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1 (1), 111–146.Google Scholar
Nadim, A., Haj-Hariri, H. & Borhan, A. 1990 Thermocapillary migration of slightly deformed droplets. Particul. Sci. Technol. 8 (3–4), 191–198.Google Scholar
Pak, O. S., Feng, J. & Stone, H. A. 2014 Viscous marangoni migration of a drop in a Poiseuille flow at low surface Péclet numbers. J. Fluid Mech. 753, 535–552.Google Scholar
Rivette, N. J. & Baygents, J. C. 1996 A note on the electrostatic force and torque acting on an isolated body in an electric field. Chem. Engng Sci. 51 (23), 5205–5211.CrossRefGoogle Scholar
Taylor, G. 1966 Studies in electrohydrodynamics. I. The circulation produced in a drop by electrical field. Proc. R. Soc. Lond. A 291 (1425), 159–166.Google Scholar
Vizika, O. & Saville, D. A. 1992 The electrohydrodynamic deformation of drops suspended in liquids in steady and oscillatory electric fields. J. Fluid Mech. 239 (1), 1–21.Google Scholar
Vlahovska, P. M. 2011 On the rheology of a dilute emulsion in a uniform electric field. J. Fluid Mec. 670, 481–503.Google Scholar
Xu, X. & Homsy, G. M. 2006 The settling velocity and shape distortion of drops in a uniform electric field. J. Fluid Mech. 564, 395–414.Google Scholar
Yariv, E. 2006 ‘Force-free’ electrophoresis? Phys. Fluids 18, 031702.CrossRefGoogle Scholar
Yariv, E. & Frankel, I. 2016 Electrohydrodynamic rotation of drops at large electric Reynolds numbers. J. Fluid Mech. 788, R2.Google Scholar