Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aslangil, Denis
Livescu, Daniel
and
Banerjee, Arindam
2019.
Progress in Turbulence VIII.
Vol. 226,
Issue. ,
p.
235.
Aslangil, Denis
Livescu, Daniel
and
Banerjee, Arindam
2020.
Variable-density buoyancy-driven turbulence with asymmetric initial density distribution.
Physica D: Nonlinear Phenomena,
Vol. 406,
Issue. ,
p.
132444.
Banerjee, Arindam
2020.
Rayleigh-Taylor Instability: A Status Review of Experimental Designs and Measurement Diagnostics.
Journal of Fluids Engineering,
Vol. 142,
Issue. 12,
Soulard, O.
Griffond, J.
Gréa, B.-J.
and
Viciconte, G.
2020.
Permanence of large eddies in decaying variable-density homogeneous turbulence with small Mach numbers.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Pereira, F. S.
Grinstein, F. F.
Israel, D. M.
Rauenzahn, R.
and
Girimaji, S. S.
2021.
Modeling and simulation of transitional Rayleigh–Taylor flow with partially averaged Navier–Stokes equations.
Physics of Fluids,
Vol. 33,
Issue. 11,
Gibbon, John D.
2021.
Variable density model for the Rayleigh-Taylor instability and its transformation to the diffusive, inhomogeneous, incompressible Navier-Stokes equations.
Physical Review Fluids,
Vol. 6,
Issue. 8,
Livescu, D.
Wei, T.
and
Brady, P.T.
2021.
Rayleigh–Taylor instability with gravity reversal.
Physica D: Nonlinear Phenomena,
Vol. 417,
Issue. ,
p.
132832.
Saenz, J. A.
Aslangil, D.
and
Livescu, D.
2021.
Filtering, averaging, and scale dependency in homogeneous variable density turbulence.
Physics of Fluids,
Vol. 33,
Issue. 2,
Zhou, Ye
Williams, Robin J.R.
Ramaprabhu, Praveen
Groom, Michael
Thornber, Ben
Hillier, Andrew
Mostert, Wouter
Rollin, Bertrand
Balachandar, S.
Powell, Phillip D.
Mahalov, Alex
and
Attal, N.
2021.
Rayleigh–Taylor and Richtmyer–Meshkov instabilities: A journey through scales.
Physica D: Nonlinear Phenomena,
Vol. 423,
Issue. ,
p.
132838.
Braun, N. O.
and
Gore, R. A.
2021.
A multispecies turbulence model for the mixing and de-mixing of miscible fluids.
Journal of Turbulence,
Vol. 22,
Issue. 12,
p.
784.
Pereira, F. S.
Grinstein, F. F.
Israel, D. M.
Rauenzahn, R.
and
Girimaji, S. S.
2021.
Partially averaged Navier-Stokes closure modeling for variable-density turbulent flow.
Physical Review Fluids,
Vol. 6,
Issue. 8,
Wong, Man Long
Baltzer, Jon R.
Livescu, Daniel
and
Lele, Sanjiva K.
2022.
Analysis of second moments and their budgets for Richtmyer-Meshkov instability and variable-density turbulence induced by reshock.
Physical Review Fluids,
Vol. 7,
Issue. 4,
Kurien, Susan
and
Pal, Nairita
2022.
The local wavenumber model for computation of turbulent mixing.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2219,
Boureima, I.
Gyrya, V.
Saenz, J.A.
Kurien, S.
and
Francois, M.
2022.
Dynamic calibration of differential equations using machine learning, with application to turbulence models.
Journal of Computational Physics,
Vol. 457,
Issue. ,
p.
110924.
Aslangil, Denis
Lawrie, Andrew G. W.
and
Banerjee, Arindam
2022.
Effects of variable deceleration periods on Rayleigh-Taylor instability with acceleration reversals.
Physical Review E,
Vol. 105,
Issue. 6,
Boffetta, G.
and
Musacchio, S.
2022.
Incompressible Rayleigh-Taylor mixing in circular and spherical geometries.
Physical Review E,
Vol. 105,
Issue. 2,
Aslangil, Denis
and
Wong, Man Long
2022.
Study of iso-thermal stratification strength on 2D multi-mode compressible Rayleigh-Taylor instability.
Walters, Stephen J.
Turner, Ross J.
and
Forbes, Lawrence K.
2022.
Computing interfacial flows of viscous fluids.
Journal of Computational Physics,
Vol. 471,
Issue. ,
p.
111626.
Tian, Yifeng
Woodward, Michael
Stepanov, Mikhail
Fryer, Chris
Hyett, Criston
Livescu, Daniel
and
Chertkov, Michael
2023.
Lagrangian large eddy simulations via physics-informed machine learning.
Proceedings of the National Academy of Sciences,
Vol. 120,
Issue. 34,
Aslangil, Denis
and
Wong, Man Long
2023.
Investigation of strong isothermal stratification effects on multi-mode compressible Rayleigh–Taylor instability.
Physics of Fluids,
Vol. 35,
Issue. 8,
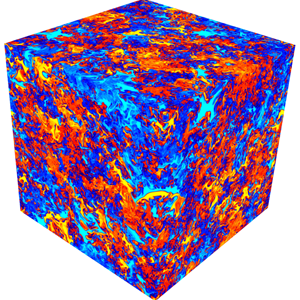
 $-7/3$ to
$-7/3$ to  $-1$, as a function of the production-to-dissipation ratio. The classical Kolmogorov spectrum emerges at intermediate to high scales at the highest Reynolds numbers examined, after the turbulence starts to decay. Finally, the similarities and differences between buoyancy-driven HVDT and the more conventional stationary turbulence are discussed and new strategies and tools for analysis are proposed.
$-1$, as a function of the production-to-dissipation ratio. The classical Kolmogorov spectrum emerges at intermediate to high scales at the highest Reynolds numbers examined, after the turbulence starts to decay. Finally, the similarities and differences between buoyancy-driven HVDT and the more conventional stationary turbulence are discussed and new strategies and tools for analysis are proposed.
