Article contents
Evolution of a turbulent cloud under rotation
Published online by Cambridge University Press: 02 September 2014
Abstract
Localized patches of turbulence frequently occur in geophysics, such as in the atmosphere and oceans. The effect of rotation, 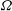 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\boldsymbol{\Omega}$ , on such a region (a ‘turbulent cloud’) is governed by inhomogeneous dynamics. In contrast, most investigations of rotating turbulence deal with the homogeneous case, although inhomogeneous turbulence is more common in practice. In this paper, we describe the results of
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\boldsymbol{\Omega}$ , on such a region (a ‘turbulent cloud’) is governed by inhomogeneous dynamics. In contrast, most investigations of rotating turbulence deal with the homogeneous case, although inhomogeneous turbulence is more common in practice. In this paper, we describe the results of 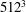 $512^3$ direct numerical simulations (DNS) of a turbulent cloud under rotation at three Rossby numbers (
$512^3$ direct numerical simulations (DNS) of a turbulent cloud under rotation at three Rossby numbers ( 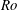 $\mathit{Ro}$ ), namely 0.1, 0.3 and 0.5. Using a spatial filter, fully developed homogeneous turbulence is vertically confined to the centre of a periodic box before the rotation is turned on. Energy isosurfaces show that columnar structures emerge from the cloud and grow into the adjacent quiescent fluid. Helicity is used as a diagnostic and confirms that these structures are formed by inertial waves. In particular, it is observed that structures growing parallel to the rotation axis (upwards) have negative helicity and those moving antiparallel (downwards) to the axis have positive helicity, a characteristic typical of inertial waves. Two-dimensional energy spectra of horizontal wavenumbers,
$\mathit{Ro}$ ), namely 0.1, 0.3 and 0.5. Using a spatial filter, fully developed homogeneous turbulence is vertically confined to the centre of a periodic box before the rotation is turned on. Energy isosurfaces show that columnar structures emerge from the cloud and grow into the adjacent quiescent fluid. Helicity is used as a diagnostic and confirms that these structures are formed by inertial waves. In particular, it is observed that structures growing parallel to the rotation axis (upwards) have negative helicity and those moving antiparallel (downwards) to the axis have positive helicity, a characteristic typical of inertial waves. Two-dimensional energy spectra of horizontal wavenumbers, 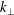 $k_{\perp }$ , versus dimensionless time,
$k_{\perp }$ , versus dimensionless time, 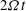 $2 \varOmega t$ , confirm that these columnar structures are wavepackets which travel at the group velocities of inertial waves. The kinetic energy transferred from the turbulent cloud to the waves is estimated using Lagrangian particle tracking to distinguish between turbulent and ‘wave-only’ regions of space. The amount of energy transferred to waves is 40 % of the initial at
$2 \varOmega t$ , confirm that these columnar structures are wavepackets which travel at the group velocities of inertial waves. The kinetic energy transferred from the turbulent cloud to the waves is estimated using Lagrangian particle tracking to distinguish between turbulent and ‘wave-only’ regions of space. The amount of energy transferred to waves is 40 % of the initial at 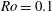 $\mathit{Ro}=0.1$ , while it is 16 % at
$\mathit{Ro}=0.1$ , while it is 16 % at 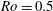 $\mathit{Ro}=0.5$ . In both cases the bulk of the energy eventually resides in the waves. It is evident from this observation that inertial waves can carry a significant portion of the energy away from a localized turbulent source and are therefore an efficient mechanism of energy dispersion.
$\mathit{Ro}=0.5$ . In both cases the bulk of the energy eventually resides in the waves. It is evident from this observation that inertial waves can carry a significant portion of the energy away from a localized turbulent source and are therefore an efficient mechanism of energy dispersion.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 24
- Cited by

