Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T07:42:15.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of the velocity gradient tensor invariant dynamics in a turbulent boundary layer

Published online by Cambridge University Press:  20 February 2017

P. Bechlars Open the ORCID record for P. Bechlars [Opens in a new window]  and
R. D. Sandberg
P. Bechlars*
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
R. D. Sandberg
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
*
†Email address for correspondence: patrick.bechlars@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

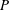In order to improve the physical understanding of the development of turbulent structures, the compressible evolution equations for the first three invariants $P$, 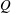$Q$ and 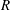$R$ of the velocity gradient tensor have been derived. The mean evolution of characteristic turbulent structure types in the 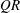$QR$-space were studied and compared at different wall-normal locations of a compressible turbulent boundary layer. The evolution of these structure types is fundamental to the physics that needs to be captured by turbulence models. Significant variations of the mean evolution are found across the boundary layer. The key features of the changes of the mean trajectories in the invariant phase space are highlighted and the consequences of the changes are discussed. Further, the individual elements of the overall evolution are studied separately to identify the causes that lead to the evolution varying with the distance to the wall. Significant impact of the wall-normal location on the coupling between the pressure-Hessian tensor and the velocity gradient tensor was found. The highlighted features are crucial for the development of more universal future turbulence models.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence modelling Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 223 - 242
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bechlars, P.2015 Comprehensive characterisation of turbulence dynamics with emphasis on wall-bounded flows. PhD thesis, University of Southampton.Google Scholar
Bechlars, P. & Sandberg, R. D. 2017 Variation of enstrophy production and strain rotation relation in a turbulent boundary layer. J. Fluid Mech. 812, 321–348.Google Scholar
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.Google Scholar
Bode, C. & Friedrichs, J. 2014 The effects of turbulence length scale on turbulence and transition prediction on turbomachinery flows. In Proceedings of the ASME Turbo Expo 2014, pp. 1–13.Google Scholar
Chacin, J. M., Cantwell, B. J. & Kline, S. J. 1996 Study of turbulent boundary layer structure using the invariants of the velocity gradient tensor. Exp. Therm. Fluid Sci. 13 (4), 308–317.Google Scholar
Chevillard, L., Meneveau, C., Biferale, L. & Toschi, F. 2008 Modeling the pressure Hessian and viscous Laplacian in turbulence: comparisons with direct numerical simulation and implications on velocity gradient dynamics. Phys. Fluids 20 (10), 101504.Google Scholar
Chong, M. S., Soria, J., Perry, a. E., Chacin, J. M., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Evolution and lifetimes of flow topology in a turbulent boundary layer. Phys. Fluids 22 (1), 015102.Google Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2014 Evolution of the velocity-gradient tensor in a spatially developing turbulent flow. J. Fluid Mech. 756, 252–292.Google Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008 Local and nonlocal strain rate fields and vorticity alignment in turbulent flows. Phys. Rev. E 77 (2), 1–8.Google ScholarPubMed
Jeong, E. & Girimaji, S. S. 2003 Velocity-gradient dynamics in turbulence: effect of viscosity and forcing. Theor. Comput. Fluid Dyn. 16, 421–432.Google Scholar
Laizet, S., Vassilicos, J. C. & Cambon, C. 2013 Interscale energy transfer in decaying turbulence and vorticity–strain-rate dynamics in grid-generated turbulence. Fluid Dyn. Res. 45 (6), 61408.Google Scholar
Lawson, J. M. & Dawson, J. R. 2015 On velocity gradient dynamics and turbulent structure. J. Fluid Mech. 780, 60–98.Google Scholar
Lozano-Durán, A., Holzner, M. & Jiménez, J. 2015 Numerically accurate computation of the conditional trajectories of the topological invariants in turbulent flows. J. Comput. Phys. 295, 805–814.Google Scholar
Luethi, B., Holzner, M. & Tsinober, A. 2009 Expanding the QR space to three dimensions. J. Fluid Mech. 641, 497–507.CrossRefGoogle Scholar
Martin, J., Ooi, A., Chong, M. S. & Soria, J. 1998 Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 10 (9), 2336.Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43 (1), 219–245.Google Scholar
Ooi, A., Martin, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19, 125–155.Google Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101 (1), 104–129.Google Scholar
Sagaut, P., Deck, S. & Terracol, M. 2013 Multiscale and Multiresolution Approaches in Turbulence – LES, DES and Hybrid RANS/LES Methods: Applications and Guidelines, 2nd edn. Imperial College Press.Google Scholar
Sandberg, R. D. 2015 Compressible-flow DNS with application to airfoil noise. Flow Turbul. Combust. 95 (2–3), 211–229.Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6, 871–884.CrossRefGoogle Scholar
Spalart, P. R. 2015 Philosophies and fallacies in turbulence modeling. Prog. Aerosp. Sci. 74, 1–15.Google Scholar
Suman, S. & Girimaji, S. S. 2013 Velocity gradient dynamics in compressible turbulence: characterization of pressure-Hessian tensor. Phys. Fluids 25 (12), 125103.Google Scholar
Thompson, K. W. 1990 Time dependent boundary conditions for hyperbolic systems, II. J. Comput. Phys. 89, 439–461.Google Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.Google Scholar
Tsinober, A. 2000 Vortex stretching versus production of strain/dissipation. Turbul. Struct. Vortex Dyn. 164–191.Google Scholar
Vieillefosse, P. 1982 Local interaction between vorticity and shear in a perfect incompressible fluid. J. Phys. 43, 836–842.Google Scholar
Vieillefosse, P. 1984 Internal motion of a small element of fluid in an inviscid flow. Physica A 125 (1), 150–162.Google Scholar
Wang, L. & Lu, X. 2012 Flow topology in compressible turbulent boundary layer. J. Fluid Mech. 703, 255–278.Google Scholar
Wilczek, M. & Meneveau, C. 2014 Pressure Hessian and viscous contributions to velocity gradient statistics based on Gaussian random fields. J. Fluid Mech. 756, 191–225.Google Scholar