Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-11T05:59:17.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of the velocity-gradient tensor in a spatially developing turbulent flow

Published online by Cambridge University Press:  01 September 2014

R. Gomes-Fernandes ,
B. Ganapathisubramani  and
J. C. Vassilicos
R. Gomes-Fernandes
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
B. Ganapathisubramani
Affiliation:
Aerodynamics & Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
J. C. Vassilicos*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: j.c.vassilicos@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

An experimental study of turbulence generated by a low-blockage space-filling fractal square grid was performed using cinematographic stereoscopic particle image velocimetry in a water tunnel. All fluctuating velocity gradients were measured and their statistics were computed at three different stations along the streamwise direction downstream of the grid: in the production region, at the location of peak turbulence intensity and in the non-equilibrium decay region. The usual signatures of these statistics are only found in the decay region, where a well-defined 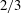$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}2/3$ power-law dependence of the second-order structure function on two-point distance is also present. However, this 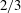$2/3$ exponent is well defined over a wide range of scales even at the peak location, where the statistics of the fluctuating velocity-gradient tensor are very unusual. There, as at the production region station, the 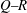$Q\text {--}R$ teardrop shape is not yet fully developed, vortex stretching only slightly dominates over compression and they both fluctuate very widely, reaching very high low-probability values. In these two stations, there is also only marginal preference between sheet-like and tube-like velocity-gradient structures as seen by the sign of the second eigenvalue of the strain-rate tensor. Yet, there are subregions of the flow in the production region where the 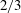$2/3$ exponent is present and where the 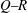$Q\text {--}R$ teardrop shape is as undeveloped as for the entire data set at this station.

JFM classification

Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 252 - 292
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343–2353.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Betchov, R. J. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1, 497–504.Google Scholar
Betchov, R. J. 1975 Numerical simulation of isotropic turbulence. Phys. Fluids 18, 1230–1236.Google Scholar
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.Google Scholar
Buxton, O. R. H. & Ganapathisubramani, B. 2010 Amplification of enstrophy in the far field of an axisymmetric turbulent jet. J. Fluid Mech. 651, 483–502.Google Scholar
Buxton, O. R. H., Laizet, S. & Ganapathisubramani, B. 2011 The effects of resolution and noise on kinematic features of fine-scale turbulence. Exp. Fluids 51, 1417–1437.CrossRefGoogle Scholar
Cantwell, B. J. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids A 4, 782–793.Google Scholar
Chacin, J. M. & Cantwell, B. J. 2000 Dynamics of a low Reynolds number turbulent boundary layer. J. Fluid Mech. 404, 87–115.CrossRefGoogle Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Discetti, S., Ziskin, I. B., Astarita, T., Adrian, R. J. & Prestridge, K. P. 2013 PIV measurements of anisotropy and inhomogeneity in decaying fractal generated turbulence. Fluid Dyn. Res. 45, 061401.Google Scholar
van Doorne, C. W. H. & Westerweel, J. 2007 Measurement of laminar, transitional and turbulent pipe flow using stereoscopic-PIV. Exp. Fluids 42, 259–279.Google Scholar
Gamba, M., Clemens, N. T. & Ezekoye, O. A. 2013 Volumetric PIV and 2D OH PLIF imaging in the far-field of a low Reynolds number non-premixed jet flame. Meas. Sci. Technol. 24, 024003.Google Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2007 Determination of complete velocity gradient tensor by using cinematographic stereoscopic PIV in a turbulent jet. Exp. Fluids 42, 923–939.CrossRefGoogle Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2012 Particle image velocimetry study of fractal-generated turbulence. J. Fluid Mech. 711, 306–336.Google Scholar
Gulitski, G., Kholmyansky, M., Kinzelbach, W., Lüthi, B., Tsinober, A. & Yorish, S. 2007 Velocity and temperature derivatives in high-Reynolds-number turbulent flows in the atmospheric surface layer. Part 1. Facilities, methods and some general results. J. Fluid Mech. 589, 57–82.CrossRefGoogle Scholar
Hurst, D. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19, 035103.Google Scholar
Jayesh,   & Warhaft, Z. 1992 Probability distribution, conditional dissipation, and transport of passive temperature fluctuations in grid-generated turbulence. Phys. Fluids A 4, 2292–2307.CrossRefGoogle Scholar
Khashehchi, M., Elsinga, G. E., Ooi, A., Soria, J. & Marusic, I. 2010 Studying invariants of the velocity gradient tensor of a round turbulent jet across the turbulent/non-turbulent interface using tomo-PIV. In Proceedings of the 15th International Symposium on Applications of Laser Techniques to Fluid Mechanics 2010, Springer.Google Scholar
Kholmyansky, M. & Tsinober, A. 2009 On an alternative explanation of anomalous scaling and how well-defined is the concept of inertial range. Phys. Lett. A 373 (27), 2364–2367.Google Scholar
Kohlmyansky, M., Tsinober, A. & Yorish, S. 2001 Velocity derivatives in the atmospheric surface layer at $\mathit{Re}_{\lambda }=10^4$ . Phys. Fluids 13, 311–314.Google Scholar
Kolmogorov, A. N. 1941a The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. C. R. Akad. Sci. SSSR 30, 301–305.Google Scholar
Kolmogorov, A. N. 1941b On degeneration of isotropic turbulence in an incompressible viscous liquid. C. R. Akad. Sci. SSSR 31, 538–540.Google Scholar
Kolmogorov, A. N. 1941c Dissipation of energy in locally isotropic turbulence. C. R. Akad. Sci. SSSR 32, 16–18.Google Scholar
Krogstad, P. Å. & Davidson, P. A. 2012 Near-field investigation of turbulence produced by multi-scale grids. Phys. Fluids 24 (3), 035103.Google Scholar
Laizet, S., Vassilicos, J. C. & Cambon, C. 2013 Interscale energy transfer in decaying turbulence and vorticity–strain rate dynamics in grid-generated turbulence. Fluid Dyn. Res. 45 (6), 061408.Google Scholar
Lundgren, T. S. 1982 Strained spiral vortex model for turbulent fine structure. Phys. Fluids 25 (12), 2193–2203.Google Scholar
Lüthi, B., Tsinober, A. & Kinzelbach, W. 2005 Lagrangian measurement of vorticity dynamics in turbulent flow. J. Fluid Mech. 528, 87–118.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22, 075101.Google Scholar
Mouri, H., Hori, A. & Takaoka, M. 2008 Fluctuations of statistics among subregions of a turbulence velocity field. Phys. Fluids 20, 035108.Google Scholar
Mullin, J. A. & Dahm, W. J. A. 2006 Dual-plane stereo particle image velocimetry measurements of velocity gradient tensor fields in turbulent shear flow. I. Accuracy assessments. Phys. Fluids 18, 035101.Google Scholar
Nagata, K., Sakai, Y., Suzuki, H., Suzuki, H., Terashima, O. & Inaba, T. 2013 Turbulence structure and turbulence kinetic energy transport in multiscale/fractal-generated turbulence. Phys. Fluids 25, 065102.Google Scholar
Ooi, M. A., Soria, J. & Chong, M. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.Google Scholar
Prasad, A. K. & Jensen, K. 1995 Scheimpflug stereocamera for particle image velocimetry in liquid flows. Appl. Opt. 34 (30), 7092–7099.Google Scholar
Raffel, M. 2007 Particle Image Velocimetry: A Practical Guide. Springer.CrossRefGoogle Scholar
Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19, 105108.Google Scholar
Simmons, L. F. G. & Salter, C. 1934 Experimental investigation and analysis of the velocity variations in turbulent flow. Proc. R. Soc. Lond. A 145 (854), 212–234.Google Scholar
Soloff, S. M., Adrian, R. J. & Liu, Z.-C. 1997 Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 8, 1441–1454.Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6, 871–884.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Steinberg, A. M., Driscoll, J. F. & Ceccio, S. L. 2008 Measurements of turbulent premixed flame dynamics using cinema stereoscopic PIV. Exp. Fluids 44, 985–999.Google Scholar
Taylor, G. I. 1938 Production and dissipation of vorticity in a turbulent fluid. Proc. R. Soc. Lond. A 164, 15–23.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Tsinober, A. 2000 Vortex stretching versus production of strain/dissipation. In Turbulence Structure and Vortex Dynamics (ed. Vassilicos, J. C. & Hunt, J. C. R.), pp. 164–191. Cambridge University Press.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence. Springer.Google Scholar
Tsinober, A., Eggels, J. G. M. & Nieuwstadt, F. T. M. 1995a On alignments and small scale structure in turbulent pipe flow. Fluid Dyn. Res. 16 (5), 297–310.Google Scholar
Tsinober, A., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity gradients in turbulent flows. J. Fluid Mech. 242, 169–192.Google Scholar
Tsinober, A., Shtilman, L., Sinyavskii, A. & Vaisburd, H. 1995b Vortex stretching and enstrophy generation in numerical and laboratory turbulence. In Small-Scale Structures in Three-Dimensional Hydrodynamic and Magnetohydrodynamic Turbulence, pp. 9–16. Springer.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multi-scale grids. J. Fluid Mech. 687, 300–340.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Universal dissipation scaling for non-equilibrium turbulence. Phys. Rev. Lett. 108, 214503.Google Scholar
Westerweel, J. 1993 Digital Particle Image Velocimetry. Delft University Press.Google Scholar
Yanitskii, V. E. 1982 Transport equation for the deformation-rate tensor and description of an ideal incompressible liquid by a system of equations of the dynamical type. Sov. Phys. Dokl. 27, 701–703.Google Scholar