Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-14T03:13:13.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of the three-dimensional flow structure around a pair of cubes immersed in the inner part of a turbulent channel flow

Published online by Cambridge University Press:  17 May 2021

Jian Gao Open the ORCID record for Jian Gao [Opens in a new window] ,
Karuna Agarwal Open the ORCID record for Karuna Agarwal [Opens in a new window]  and
Joseph Katz Open the ORCID record for Joseph Katz [Opens in a new window]
Jian Gao
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD21218, USA
Karuna Agarwal
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD21218, USA
Joseph Katz*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD21218, USA
*
†Email address for correspondence: katz@jhu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

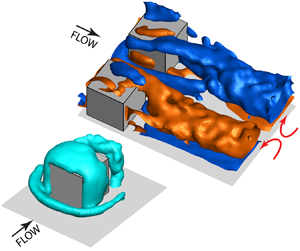
The origin and evolution of the three-dimensional flow structures around a pair of roughness cubes embedded in the inner part of a turbulent channel flow (${\textit{Re}}_{\tau \infty }=2300$, where ${\textit{Re}}_{\tau \infty}$ is the friction Reynolds number of the incoming turbulent channel flow) are measured using microscopic dual-view tomographic holography. The cubes’ height, $a=1$ mm, corresponds to 91 wall units or 3.9 % of the half-channel height. They are aligned in the spanwise direction and separated by a, 1.5a and 2.5a. This paper focuses on the mean flow structure, and the data resolution allows detailed characterization of the open separated regions upstream, along the sides, on top of and behind the cubes, as well as measurements of wall shear stresses from velocity gradients. The flow features a horseshoe vortex, a vortical canopy engulfing each cube, a near wake arch-like vortex and multiple interacting streamwise vortices. Most of the boundary layer vorticity is entrained into the horseshoe vortex. The canopy, consisting of wall-normal vorticity to the sides, and spanwise vorticity on top of the cube, originates from the front surface. The streamwise vortices originate from realignment of the other components along the corners of the front surface. Merging of streamwise structures around and behind each cube causes formation of a large streamwise vortex rotating in the same direction as the inner horseshoe leg, with remnants of the outer leg under it. This merging occurs earlier and the entire flow structure becomes more asymmetric with decreasing spacing. Peaks and minima in the distributions of the wall shear stress are associated with the formation of and interactions among the near-wall vortices.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 918 , 10 July 2021 , A31
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahn, J., Lee, J.H. & Sung, H.J. 2013 Statistics of the turbulent boundary layers over 3D cube-roughened walls. Intl J. Heat Fluid Flow 44, 394–402.CrossRefGoogle Scholar
Bai, K. & Katz, J. 2014 On the refractive index of sodium iodide solutions for index matching in PIV. Exp. Fluids 55, 1704.CrossRefGoogle Scholar
Bakken, O.M., Krogstad, P., Ashrafian, A. & Andersson, H.I. 2005 Reynolds number effects in the outer layer of the turbulent flow in a channel with rough walls. Phys. Fluids 17 (6), 065101.CrossRefGoogle Scholar
Barros, J.M. & Christensen, K.T. 2014 Observations of turbulent secondary flows in a rough-wall boundary layer. J. Fluid Mech. 748, R1.CrossRefGoogle Scholar
Blackman, K., Perret, L., Calmet, I. & Rivet, C. 2017 Turbulent kinetic energy budget in the boundary layer developing over an urban-like rough wall using PIV. Phys. Fluids 29 (8), 085113.CrossRefGoogle Scholar
Castro, I.P. & Robins, A.G. 1977 The flow around a surface-mounted cube in uniform and turbulent streams. J. Fluid Mech. 79 (2), 307–335.CrossRefGoogle Scholar
Choi, Y.K., Hwang, H.G., Lee, Y.M. & Lee, J.H. 2020 Effects of the roughness height in turbulent boundary layers over rod- and cuboid-roughened walls. Intl J. Heat Fluid Flow 85, 108644.CrossRefGoogle Scholar
Coceal, O., Dobre, A., Thomas, T.G. & Belcher, S.E. 2007 Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 589, 375–409.CrossRefGoogle Scholar
Devenport, W., Alexander, N., Glegg, S. & Wang, M. 2018 The sound of flow over rigid walls. Annu. Rev. Fluid Mech. 50 (1), 435–458.CrossRefGoogle Scholar
Diaz-Daniel, C., Laizet, S. & Vassilicos, J.C. 2017 Direct numerical simulations of a wall-attached cube immersed in laminar and turbulent boundary layers. Intl J. Heat Fluid Flow 68, 269–280.CrossRefGoogle Scholar
Flack, K.A., Schultz, M.P. & Connelly, J.S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.CrossRefGoogle Scholar
Gao, J. & Katz, J. 2018 Self-calibrated microscopic dual-view tomographic holography for 3D flow measurements. Opt. Express 26 (13), 16708–16725.CrossRefGoogle ScholarPubMed
George, J. 2005 Structure of 2-D and 3-D turbulent boundary layers with sparsely distributed roughness elements. PhD thesis, Virginia Tech, VA.CrossRefGoogle Scholar
Hearst, R.J., Gomit, G. & Ganapathisubramani, B. 2016 Effect of turbulence on the wake of a wall-mounted cube. J. Fluid Mech. 804, 513–530.CrossRefGoogle Scholar
Hong, J., Katz, J., Meneveau, C. & Schultz, M.P. 2012 Coherent structures and associated subgrid-scale energy transfer in a rough-wall turbulent channel flow. J. Fluid Mech. 712, 92–128.CrossRefGoogle Scholar
Hong, J., Katz, J. & Schultz, M.P. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.CrossRefGoogle Scholar
Hunt, J.C.R., Abell, C.J., Peterka, J.A. & Woo, H. 1978 Kinematical studies of the flows around free or surface-mounted obstacles; applying topology to flow visualization. J. Fluid Mech. 86 (1), 179–200.CrossRefGoogle Scholar
Hussein, H.J. & Martinuzzi, R.J. 1996 Energy balance for turbulent flow around a surface mounted cube placed in a channel. Phys. Fluids 8 (3), 764–780.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.CrossRefGoogle Scholar
Joshi, P., Liu, X. & Katz, J. 2014 Effect of mean and fluctuating pressure gradients on boundary layer turbulence. J. Fluid Mech. 748, 36–84.CrossRefGoogle Scholar
Katz, J. & Sheng, J. 2010 Applications of holography in fluid mechanics and particle dynamics. Annu. Rev. Fluid Mech. 42 (1), 531–555.CrossRefGoogle Scholar
Krogstad, P.A. & Antonia, R.A. 1999 Surface roughness effects in turbulent boundary layers. Exp. Fluids 27, 450–460.CrossRefGoogle Scholar
Lee, J.H., Sung, H.J. & Krogstad, P. 2011 Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 669, 397–431.CrossRefGoogle Scholar
Leonardi, S. & Castro, I.P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.CrossRefGoogle Scholar
Lim, H.C., Thomas, T.G. & Castro, I.P. 2009 Flow around a cube in a turbulent boundary layer: LES and experiment. J. Wind Engng Ind. Aerodyn. 97 (2), 96–109.CrossRefGoogle Scholar
Ling, H., Srinivasan, S., Golovin, K., McKinley, G.H., Tuteja, A. & Katz, J. 2016 High-resolution velocity measurement in the inner part of turbulent boundary layers over super-hydrophobic surfaces. J. Fluid Mech. 801, 670–703.CrossRefGoogle Scholar
Martinuzzi, R. & Tropea, C. 1993 The flow around surface-mounted, prismatic obstacles placed in a fully developed channel flow (data bank contribution). Trans. ASME: J. Fluids Engng 115 (1), 85–92.Google Scholar
Marusic, I., McKeon, B.J., Monkewitz, P.A., Nagib, H.M., Smits, A.J. & Sreenivasan, K.R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.CrossRefGoogle Scholar
Mejia-Alvarez, R. & Christensen, K.T. 2013 Wall-parallel stereo particle-image velocimetry measurements in the roughness sublayer of turbulent flow overlying highly irregular roughness. Phys. Fluids 25 (11), 115109.CrossRefGoogle Scholar
Piomelli, U. 2019 Recent advances in the numerical simulation of rough-wall boundary layers. Phys. Chem. Earth 113, 63–72.CrossRefGoogle Scholar
Raupach, M.R., Antonia, R.A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.CrossRefGoogle Scholar
Reynolds, R.T. & Castro, I.P. 2008 Measurements in an urban-type boundary layer. Exp. Fluids 45, 141–156.CrossRefGoogle Scholar
Schröder, A., Willert, C., Schanz, D., Geisler, R., Jahn, T., Gallas, Q. & Leclaire, B. 2020 The flow around a surface mounted cube: a characterization by time-resolved PIV, 3D Shake-The-Box and LBM simulation. Exp. Fluids 61, 189.CrossRefGoogle Scholar
Sheng, J., Malkiel, E. & Katz, J. 2008 Using digital holographic microscopy for simultaneous measurements of 3D near wall velocity and wall shear stress in a turbulent boundary layer. Exp. Fluids 45, 1023–1035.CrossRefGoogle Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.CrossRefGoogle Scholar
da Silva, B.L., Chakravarty, R., Sumner, D. & Bergstrom, D.J. 2020 Aerodynamic forces and three-dimensional flow structures in the mean wake of a surface-mounted finite-height square prism. Intl J. Heat Fluid Flow 83, 108569.CrossRefGoogle Scholar
Simpson, R.L. 2001 Junction flows. Annu. Rev. Fluid Mech. 33 (1), 415–443.CrossRefGoogle Scholar
Sousa, J.M.M. 2002 Turbulent flow around a surface-mounted obstacle using 2D-3C DPIV. Exp. Fluids 33, 854–862.CrossRefGoogle Scholar
Squire, D.T., Morrill-Winter, C., Hutchins, N., Schultz, M.P., Klewicki, J.C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.CrossRefGoogle Scholar
Takimoto, H., Sato, A., Barlow, J.F., Moriwaki, R., Inagaki, A., Onomura, S. & Kanda, M. 2011 Particle image velocimetry measurements of turbulent flow within outdoor and indoor urban scale models and flushing motions in urban canopy layers. Boundary-Layer Meteorol. 140, 295–314.CrossRefGoogle Scholar
Talapatra, S. & Katz, J. 2012 Coherent structures in the inner part of a rough-wall channel flow resolved using holographic PIV. J. Fluid Mech. 711, 161–170.CrossRefGoogle Scholar
Talapatra, S. & Katz, J. 2013 Three-dimensional velocity measurements in a roughness sublayer using microscopic digital in-line holography and optical index matching. Meas. Sci. Technol. 24 (2), 024004.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Volino, R.J., Schultz, M.P. & Flack, K.A. 2011 Turbulence structure in boundary layers over periodic two- and three-dimensional roughness. J. Fluid Mech. 676, 172–190.CrossRefGoogle Scholar
Westerweel, J., Elsinga, G.E. & Adrian, R.J. 2013 Particle image velocimetry for complex and turbulent flows. Annu. Rev. Fluid Mech. 45 (1), 409–436.CrossRefGoogle Scholar
Wu, S., Christensen, K.T. & Pantano, C. 2020 A study of wall shear stress in turbulent channel flow with hemispherical roughness. J. Fluid Mech. 885, A16.CrossRefGoogle Scholar
Yakhot, A., Liu, H. & Nikitin, N. 2006 Turbulent flow around a wall-mounted cube: a direct numerical simulation. Intl J. Heat Fluid Flow 27 (6), 994–1009.CrossRefGoogle Scholar
Yang, Q. & Wang, M. 2013 Boundary-layer noise induced by arrays of roughness elements. J. Fluid Mech. 727, 282–317.CrossRefGoogle Scholar
Yang, X.I.A., Xu, H.H.A., Huang, X.L.D. & Ge, M.-W. 2019 Drag forces on sparsely packed cube arrays. J. Fluid Mech. 880, 992–1019.CrossRefGoogle Scholar
Zhang, C., Wang, J., Blake, W. & Katz, J. 2017 Deformation of a compliant wall in a turbulent channel flow. J. Fluid Mech. 823, 345–390.CrossRefGoogle Scholar