Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T01:49:21.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of turbulent suspensions of spherical particles in a square duct

Published online by Cambridge University Press:  26 October 2018

Sagar Zade ,
Pedro Costa Open the ORCID record for Pedro Costa [Opens in a new window] ,
Walter Fornari Open the ORCID record for Walter Fornari [Opens in a new window] ,
Fredrik Lundell  and
Luca Brandt Open the ORCID record for Luca Brandt [Opens in a new window]
Sagar Zade
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
Pedro Costa
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
Walter Fornari
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
Fredrik Lundell
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
Luca Brandt*
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
*
†Email address for correspondence: luca@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

We report experimental observations of turbulent flow with spherical particles in a square duct. Three particle sizes, namely 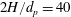$2H/d_{p}=40$, 16 and 9 (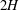$2H$ being the duct full height and 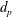$d_{p}$ being the particle diameter), are investigated. The particles are nearly neutrally buoyant with a density ratio of 1.0035 and 1.01 with respect to the suspending fluid. Refractive index matched–particle image velocimetry (RIM–PIV) is used for fluid velocity measurement even at the highest particle volume fraction (20 %) and particle tracking velocimetry (PTV) for the particle velocity statistics for the flows seeded with particles of the two largest sizes, whereas only pressure measurements are reported for the smallest particles. Settling effects are seen at the lowest bulk Reynolds number $Re_{2H}\approx$ 10 000, whereas, at the highest 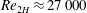$Re_{2H}\approx 27\,000$, particles are in almost full suspension. The friction factor of the suspensions is found to be significantly larger than that of single-phase duct flow at the lower 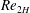$Re_{2H}$ investigated; however, the difference decreases when increasing the flow rate and the total drag approaches the values of the single-phase flow at the higher Reynolds number considered, 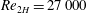$Re_{2H}=27\,000$. The pressure drop is found to decrease with the particle diameter for volume fractions lower than $\unicode[STIX]{x1D719}=10\,\%$ for nearly all 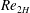$Re_{2H}$ investigated. However, at the highest volume fraction 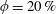$\unicode[STIX]{x1D719}=20\,\%$, we report a peculiar non-monotonic behaviour: the pressure drop first decreases and then increases with increasing particle size. The decrease of the turbulent drag with particle size at the lowest volume fractions is related to an attenuation of the turbulence. The drag increase for the two largest particle sizes at 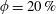$\unicode[STIX]{x1D719}=20\,\%$, however, occurs despite this large reduction of the turbulent stresses, and it is therefore due to significant particle-induced stresses. At the lowest Reynolds number, the particles reside mostly in the bottom half of the duct, where the mean velocity significantly decreases; the flow is similar to that in a moving porous bed near the bottom wall and to turbulent duct flow with low particle concentration near the top wall.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 857 , 25 December 2018 , pp. 748 - 783
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbas, M., Magaud, P., Gao, Y. & Geoffroy, S. 2014 Migration of finite sized particles in a laminar square channel flow from low to high Reynolds numbers. Phys. Fluids 26 (12), 123301.Google Scholar
Abbas, M., Pouplin, A., Masbernat, O., Liné, A. & Décarre, S. 2017 Pipe flow of a dense emulsion: homogeneous shear-thinning or shear-induced migration? AIChE J. 63 (11), 5182–5195.Google Scholar
Ardekani, M. N., Costa, P., Breugem, W.-P., Picano, F. & Brandt, L. 2017 Drag reduction in turbulent channel flow laden with finite-size oblate spheroids. J. Fluid Mech. 816, 43–70.Google Scholar
Bagnold, R. A. 1954 Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. Lond. A 225, 49–63.Google Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41 (3), 545–570.Google Scholar
Bellani, G., Byron, M. L., Collignon, A. G., Meyer, C. R. & Variano, E. A. 2012 Shape effects on turbulent modulation by large nearly neutrally buoyant particles. J. Fluid Mech. 712, 41–60.Google Scholar
Blanc, F., Lemaire, E., Meunier, A. & Peters, F. 2013 Microstructure in sheared non-Brownian concentrated suspensions. J. Rheol. 57 (1), 273–292.Google Scholar
Brundrett, E. & Baines, W. D. 1964 The production and diffusion of vorticity in duct flow. J. Fluid Mech. 19 (3), 375–394.Google Scholar
Byron, M. L. & Variano, E. A. 2013 Refractive-index-matched hydrogel materials for measuring flow–structure interactions. Exp. Fluids 54 (2), 1456.Google Scholar
Choi, Y.-S., Seo, K.-W. & Lee, S.-J. 2011 Lateral and cross-lateral focusing of spherical particles in a square microchannel. Lab on a Chip 11 (3), 460–465.Google Scholar
Chun, B. & Ladd, A. J. C. 2006 Inertial migration of neutrally buoyant particles in a square duct: an investigation of multiple equilibrium positions. Phys. Fluids 18 (3), 031704.Google Scholar
Costa, P., Picano, F., Brandt, L. & Breugem, W.-P. 2016 Universal scaling laws for dense particle suspensions in turbulent wall-bounded flows. Phys. Rev. Lett. 117 (13), 134501.Google Scholar
Costa, P., Picano, F., Brandt, L. & Breugem, W.-P. 2018 Effects of the finite particle size in turbulent wall-bounded flows of dense suspensions. J. Fluid Mech. 843, 450–478.Google Scholar
Crowe, C. T., Schwarzkopf, J. D., Sommerfeld, M. & Tsuji, Y. 2011 Multiphase Flows with Droplets and Particles. CRC Press.Google Scholar
Cuccia, N. L.2017 The tribological properties of polyacrylamide hydrogel particles. Honours thesis, Emory University. http://pid.emory.edu/ark:/25593/rzwwz.Google Scholar
Demuren, A. O. 1991 Calculation of turbulence-driven secondary motion in ducts with arbitrary cross section. AIAA J. 29 (4), 531–537.Google Scholar
Doron, P., Granica, D. & Barnea, D. 1987 Slurry flow in horizontal pipes: experimental and modeling. Intl J. Multiphase Flow 13 (4), 535–547.Google Scholar
Draad, A. A., Kuiken, G. D. C. & Nieuwstadt, F. T. M. 1998 Laminar–turbulent transition in pipe flow for Newtonian and non-Newtonian fluids. J. Fluid Mech. 377, 267–312.Google Scholar
Duan, Z., Yovanovich, M. M. & Muzychka, Y. S. 2012 Pressure drop for fully developed turbulent flow in circular and noncircular ducts. Trans. ASME J. Fluids Engng 134 (6), 061201.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Einstein, A. 1906 Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 324 (2), 289–306.Google Scholar
Einstein, A. 1911 Berichtigung zu meiner Arbeit. I. Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 339 (3), 591–592.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two-way interaction between homogeneous turbulence and dispersed solid particles. Part I. Turbulence modification. Phys. Fluids A 5 (7), 1790–1801.Google Scholar
Fornari, W., Brandt, L., Chaudhuri, P., Lopez, C. U., Mitra, D. & Picano, F. 2016a Rheology of confined non-Brownian suspensions. Phys. Rev. Lett. 116 (1), 018301.Google Scholar
Fornari, W., Formenti, A., Picano, F. & Brandt, L. 2016b The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions. Phys. Fluids 28 (3), 033301.Google Scholar
Fornari, W., Kazerooni, H. T., Hussong, J. & Brandt, L. 2018a Suspensions of finite-size neutrally buoyant spheres in turbulent duct flow. J. Fluid Mech. 851, 148–186.Google Scholar
Fornari, W., Picano, F. & Brandt, L. 2018b The effect of polydispersity in a turbulent channel flow laden with finite-size particles. Eur. J. Mech. (B/Fluids) 67, 54–64.Google Scholar
Frank, M., Anderson, D., Weeks, E. R. & Morris, J. F. 2003 Particle migration in pressure-driven flow of a Brownian suspension. J. Fluid Mech. 493, 363–378.Google Scholar
Fredsøe, J. & Deigaard, R. 1992 Mechanics of Coastal Sediment Transport. World Scientific.Google Scholar
Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.Google Scholar
Gessner, F. B. 1973 The origin of secondary flow in turbulent flow along a corner. J. Fluid Mech. 58 (1), 1–25.Google Scholar
Gong, J., Higa, M., Iwasaki, Y., Katsuyama, Y. & Osada, Y. 1997 Friction of gels. J. Phys. Chem. B 101 (28), 5487–5489.Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics. Cambridge University Press.Google Scholar
Gurung, A. & Poelma, C. 2016 Measurement of turbulence statistics in single-phase and two-phase flows using ultrasound imaging velocimetry. Exp. Fluids 57 (11), 171.Google Scholar
Hampton, R. E., Mammoli, A. A., Graham, A. L., Tetlow, N. & Altobelli, S. A. 1997 Migration of particles undergoing pressure-driven flow in a circular conduit. J. Rheol. 41 (3), 621–640.Google Scholar
Han, M., Kim, C., Kim, M. & Lee, S. 1999 Particle migration in tube flow of suspensions. J. Rheol. 43 (5), 1157–1174.Google Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65 (2), 365–400.Google Scholar
Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.Google Scholar
Kaushal, D. R. & Tomita, Y. 2002 Solids concentration profiles and pressure drop in pipeline flow of multisized particulate slurries. Intl J. Multiphase Flow 28 (10), 1697–1717.Google Scholar
Kawata, T. & Obi, S. 2014 Velocity–pressure correlation measurement based on planar PIV and miniature static pressure probes. Exp. Fluids 55 (7), 1776.Google Scholar
Kazerooni, H. T., Fornari, W., Hussong, J. & Brandt, L. 2017 Inertial migration in dilute and semidilute suspensions of rigid particles in laminar square duct flow. Phys. Rev. Fluids 2, 084301.Google Scholar
Klein, S., Gibert, M., Bérut, A. & Bodenschatz, E. 2012 Simultaneous 3D measurement of the translation and rotation of finite-size particles and the flow field in a fully developed turbulent water flow. Meas. Sci. Technol. 24 (2), 024006.Google Scholar
Koh, C. J., Hookham, P. & Leal, L. G. 1994 An experimental investigation of concentrated suspension flows in a rectangular channel. J. Fluid Mech. 266, 1–32.Google Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 277, 109–134.Google Scholar
Kulkarni, P. M. & Morris, J. F. 2008 Suspension properties at finite Reynolds number from simulated shear flow. Phys. Fluids 20 (4), 040602.Google Scholar
Lashgari, I., Picano, F., Breugem, W.-P. & Brandt, L. 2014 Laminar, turbulent, and inertial shear-thickening regimes in channel flow of neutrally buoyant particle suspensions. Phys. Rev. Lett. 113 (25), 254502.Google Scholar
Lashgari, I., Picano, F., Breugem, W. P. & Brandt, L. 2016 Channel flow of rigid sphere suspensions: particle dynamics in the inertial regime. Intl J. Multiphase Flow 78, 12–24.Google Scholar
Lin, Z., Yu, Z., Shao, X. & Wang, L.-P. 2017 Effects of finite-size neutrally buoyant particles on the turbulent flows in a square duct. Phys. Fluids 29 (10), 103304.Google Scholar
Loisel, V., Abbas, M., Masbernat, O. & Climent, E. 2013 The effect of neutrally buoyant finite-size particles on channel flows in the laminar–turbulent transition regime. Phys. Fluids 25 (12), 123304.Google Scholar
Lyon, M. K. & Leal, L. G. 1998 An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 1. Monodisperse systems. J. Fluid Mech. 363, 25–56.Google Scholar
Manoorkar, S., Krishnan, S., Sedes, O., Shaqfeh, E. S., Iaccarino, G. & Morris, J. F. 2018 Suspension flow through an asymmetric T-junction. J. Fluid Mech. 844, 247–273.Google Scholar
Matas, J.-P., Glezer, V., Guazzelli, É. & Morris, J. F. 2004a Trains of particles in finite-Reynolds-number pipe flow. Phys. Fluids 16 (11), 4192–4195.Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, É. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90 (1), 014501.Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, É. 2004b Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 515, 171–195.Google Scholar
Miura, K., Itano, T. & Sugihara-Seki, M. 2014 Inertial migration of neutrally buoyant spheres in a pressure-driven flow through square channels. J. Fluid Mech. 749, 320–330.Google Scholar
Morris, J. F. 2009 A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 48 (8), 909–923.Google Scholar
Nikuradse, J. 1930 Untersuchungen über turbulente Strömungen in nicht kreisförmigen Rohren. Ing.-Arch. 1 (3), 306–332.Google Scholar
Noorani, A., Vinuesa, R., Brandt, L. & Schlatter, P. 2016 Aspect ratio effect on particle transport in turbulent duct flows. Phys. Fluids 28 (11), 115103.Google Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.Google Scholar
Picano, F., Breugem, W.-P., Mitra, D. & Brandt, L. 2013 Shear thickening in non-Brownian suspensions: an excluded volume effect. Phys. Rev. Lett. 111 (9), 098302.Google Scholar
Poelma, C., Westerweel, J. & Ooms, G. 2006 Turbulence statistics from optical whole-field measurements in particle-laden turbulence. Exp. Fluids 40 (3), 347–363.Google Scholar
Prandtl, L. 1926 Über die ausgebildete Turbulenz. In Proceedings of the 2nd International Congress for Applied Mechanics, Zurich. NACA Tech. Mem. 62, 435 (English translation).Google Scholar
Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J. 2013 Particle Image Velocimetry: A Practical Guide. Springer.Google Scholar
Reeks, M. W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aerosol. Sci. 14 (6), 729–739.Google Scholar
Rouse, H. 1937 Modern conceptions of the mechanics of turbulence. Trans. Am. Soc. Civil Engng 102, 463–505.Google Scholar
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C. M. 2012 Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.Google Scholar
Segré, G. & Silberberg, A. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 2. Experimental results and interpretation. J. Fluid Mech. 14 (1), 136–157.Google Scholar
Sharma, G. & Phares, D. J. 2006 Turbulent transport of particles in a straight square duct. Intl J. Multiphase Flow 32 (7), 823–837.Google Scholar
Shields, A. 1936 Application of Similarity Principles and Turbulence Research to Bed-Load Movement. CalTech Library.Google Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35 (9), 827–839.Google Scholar
Squires, K. D. & Eaton, J. K. 1990 Particle response and turbulence modification in isotropic turbulence. Phys. Fluids 2 (7), 1191–1203.Google Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.Google Scholar
Uhlmann, M., Pinelli, A., Kawahara, G. & Sekimoto, A. 2007 Marginally turbulent flow in a square duct. J. Fluid Mech. 588, 153–162.Google Scholar
Wereley, S. & Gui, L. 2003 A correlation-based central difference image correction (CDIC) method and application in a four-roll mill flow PIV measurement. Exp. Fluids 34 (1), 42–51.Google Scholar
Wiederseiner, S., Andreini, N., Epely-Chauvin, G. & Ancey, C. 2011 Refractive-index and density matching in concentrated particle suspensions: a review. Exp. Fluids 50 (5), 1183–1206.Google Scholar
Winkler, C. M., Rani, S. L. & Vanka, S. P. 2004 Preferential concentration of particles in a fully developed turbulent square duct flow. Intl J. Multiphase Flow 30 (1), 27–50.Google Scholar
Yao, J., Fairweather, M. & Zhao, Y. L. 2014 Numerical simulation of particle deposition in turbulent duct flows. Ind. Engng Chem. Res. 53 (8), 3329–3341.Google Scholar
Yeo, K. & Maxey, M. R. 2013 Dynamics and rheology of concentrated, finite-Reynolds-number suspensions in a homogeneous shear flow. Phys. Fluids 25 (5), 053303.Google Scholar
Yuen, H. K., Princen, J., Illingworth, J. & Kittler, J. 1990 Comparative study of Hough transform methods for circle finding. Image Vis. Comput. 8 (1), 71–77.Google Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. Jr. 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44 (2), 185–220.Google Scholar
Zhao, L. H., Andersson, H. I. & Gillissen, J. J. J. 2010 Turbulence modulation and drag reduction by spherical particles. Phys. Fluids 22 (8), 081702.Google Scholar