Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-11T00:33:02.523Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow criticality governs leading-edge-vortex initiation on finite wings in unsteady flow

Published online by Cambridge University Press:  08 January 2021

Yoshikazu Hirato ,
Minao Shen Open the ORCID record for Minao Shen [Opens in a new window] ,
Ashok Gopalarathnam Open the ORCID record for Ashok Gopalarathnam [Opens in a new window]  and
Jack R. Edwards
Yoshikazu Hirato
Affiliation:
Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC27695, USA
Minao Shen
Affiliation:
Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC27695, USA
Ashok Gopalarathnam*
Affiliation:
Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC27695, USA
Jack R. Edwards
Affiliation:
Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC27695, USA
*
†Email address for correspondence: agopalar@ncsu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

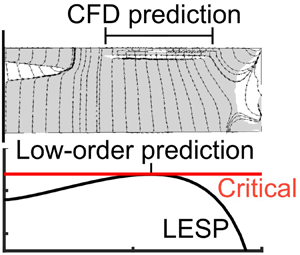
Leading-edge-vortex (LEV) formation often characterizes the unsteady flows past airfoils and wings. Recent research showed that initiation of LEV formation on airfoils in two-dimensional flow is closely tied to the criticality of the so-called leading-edge suction parameter (LESP). To characterize the LEV initiation on wings in three-dimensional flow, a large set of pitching wings was studied using Reynolds-averaged Navier–Stokes computations (computational fluid dynamics, CFD). The CFD results showed that the pitch angle and spanwise location for LEV initiation varied widely between the different wings. The same cases were also analysed using an unsteady vortex-lattice method (UVLM), which assumes attached flow. Low-order prediction of LEV initiation is assumed to occur at the pitch angle when the UVLM-calculated LESP at any point on the wing span first becomes equal to the pre-determined critical LESP for the airfoil. For all the cases, the predicted pitch angles and spanwise locations for LEV initiation from the low-order method agreed excellently with the corresponding CFD predictions. These observations show that LEV initiation on finite wings is governed by criticality of leading-edge suction, enabling the prediction of LEV initiation on an unsteady finite wing using attached-flow wing theory and the critical LESP values for the airfoil sections.

JFM classification

Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex shedding Boundary Layers: Boundary layer separation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 910 , 10 March 2021 , A1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Acharya, M. & Metwally, M. H. 1992 Unsteady pressure field and vorticity production over a pitching airfoil. AIAA J. 30 (2), 403–411.CrossRefGoogle Scholar
Aggarwal, S. 2013 An inviscid numerical method for unsteady flows over airfoils and wings to predict the onset of leading edge vortex formation. Master's thesis, North Carolina State University.Google Scholar
Anderson, J. D. 2017 Fundamentals of Aerodynamics, 6th edn. McGraw-Hill Education.Google Scholar
Ansari, S. A., Żbikowski, R. & Knowles, K. 2006 a A nonlinear unsteady aerodynamic model for insect-like flapping wings in the hover. Part 1. Methodology and analysis. Proc. Inst. Mech. Engrs 220 (2), 61–83.CrossRefGoogle Scholar
Ansari, S. A., Żbikowski, R. & Knowles, K. 2006 b A nonlinear unsteady aerodynamic model for insect-like flapping wings in the hover. Part 2. Implementation and validation. Proc. Inst. Mech. Engrs 220, 169–186.CrossRefGoogle Scholar
Beddoes, T. S. 1978 Onset of leading-edge separation effects under dynamic conditions and low Mach number. In 34th Annual Forum of the American Helicopter Society, vol. 17. American Helicopter Society.Google Scholar
Bottom, R. G. II, Borazjani, I., Blevins, E. L. & Lauder, G. V. 2016 Hydrodynamics of swimming in stingrays: numerical simulations and the role of the leading-edge vortex. J. Fluid Mech. 788, 407–443.CrossRefGoogle Scholar
Carr, L. W. 1988 Progress in analysis and prediction of dynamic stall. J. Aircraft 25 (1), 6–17.CrossRefGoogle Scholar
Cassidy, D. A., Edwards, J. R. & Tian, M. 2009 An investigation of interface-sharpening schemes for multiphase mixture flows. J. Comput. Phys. 228 (16), 5628–5649.CrossRefGoogle Scholar
Colella, P. & Woodward, P. R. 1984 The piecewise parabolic method (ppm) for gas-dynamic simulations. J. Comput. Phys. 54, 174–201.CrossRefGoogle Scholar
Corke, T. C. & Thomas, F. O. 2015 Dynamic stall in pitching airfoils: aerodynamics damping and compressibility effects. Annu. Rev. Fluid Mech. 47, 479–505.CrossRefGoogle Scholar
Dickinson, M. H. & Götz, K. G. 1993 Unsteady aerodynamic performance of model wings at low Reynolds numbers. J. Expl Biol. 174, 45–64.Google Scholar
Edwards, J. R. & Chandra, S. 1996 Comparison of eddy viscosity-transport turbulence models for three-dimensional, shock-separated flowfields. AIAA J. 34 (4), 756–763.CrossRefGoogle Scholar
Ekaterinaris, J. A. & Platzer, M. F. 1998 Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 33 (11–12), 759–846.CrossRefGoogle Scholar
Ellington, C. P. 1999 The novel aerodynamics of insect flight: applications to micro-air vehicles. J. Expl Biol. 202 (23), 3439–3448.Google ScholarPubMed
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384, 626–630.CrossRefGoogle Scholar
Ericsson, L. E. 1988 Moving wall effects in unsteady flow. J. Aircraft 25 (11), 977–990.CrossRefGoogle Scholar
Evans, W. T. & Mort, K. W. 1959 Analysis of computed flow parameters for a set of sudden stalls in low speed two-dimensional flow. NACA Tech. Rep. TN D-85. National Advisory Committee for Aeronautics.Google Scholar
Freymuth, P. 1988 Three-dimensional vortex systems of finite wings. J. Aircraft 25 (10), 971–972.CrossRefGoogle Scholar
Gault, D. E. 1957 A correlation of low-speed, airfoil-section stalling characteristics with Reynolds number and airfoil geometry. NACA Tech. Rep. TN 3963. National Advisory Committee for Aeronautics.Google Scholar
Ghosh Choudhuri, P. & Knight, D. D. 1996 Effects of compressibility, pitch rate, and Reynolds number on unsteady incipient leading-edge boundary layer separation over a pitching airfoil. J. Fluid Mech. 308, 195–217.CrossRefGoogle Scholar
Ghosh Choudhuri, P., Knight, D. D. & Visbal, M. R. 1994 Two-dimensional unsteady leading-edge separation on a pitching airfoil. AIAA J. 32 (4), 673–681.CrossRefGoogle Scholar
Gordnier, R. E. & Demasi, L. 2013 Implicit LES simulations of a flapping wing in forward flight. In FEDSM 2013-16540. ASME 2013 Fluids Engineering Division Summer Meeting. American Society of Mechanical Engineers.CrossRefGoogle Scholar
Granlund, K., Ol, M. & Bernal, L. 2011 Experiment on pitching plates: force and flowfield measurements at low Reynolds numbers. AIAA Paper 2011-872.Google Scholar
Granlund, K. O., Ol, M. V. & Bernal, L. P. 2013 Unsteady pitching flat plates. J. Fluid Mech. 733, R5.CrossRefGoogle Scholar
Gupta, R. & Ansell, P. J. 2019 Unsteady flow physics of airfoil dynamic stall. AIAA J. 57 (1), 165–175.CrossRefGoogle Scholar
Gursul, I., Gordnier, R. & Visbal, M. 2005 Unsteady aerodynamics of nonslender delta wings. Prog. Aerosp. Sci. 41 (7), 515–557.CrossRefGoogle Scholar
Ham, N. D. & Garelick, M. S. 1968 Dynamic stall considerations in helicopter rotors. J. Am. Helicopter Soc. 13, 49–55.CrossRefGoogle Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2014 The role of advance ratio and aspect ratio in determining leading-edge vortex stability for flapping flight. J. Fluid Mech. 751, 71–105.CrossRefGoogle Scholar
Hirato, Y. 2016 Leading-edge-vortex formation on finite wings in unsteady flow. PhD thesis, North Carolina State University.CrossRefGoogle Scholar
Hirato, Y., Shen, M., Gopalarathnam, A. & Edwards, J. R. 2019 Vortex-sheet representation of leading-edge vortex shedding from finite wings. J. Aircraft 56 (4), 1626–1640.CrossRefGoogle Scholar
Hitzel, S. M. & Schmidt, W. 1984 Slender wings with leading-edge vortex separation: a challenge for panel methods and euler solvers. J. Aircraft 21 (10), 751–759.CrossRefGoogle Scholar
Jantzen, R. T., Taira, K., Granlund, K. O. & Ol, M. V. 2014 Vortex dynamics around pitching plates. Phys. Fluids 26 (5), 053606.CrossRefGoogle Scholar
Johnson, W. & Ham, N. D. 1972 On the mechanism of dynamic stall. J. Am. Helicopter Soc. 17, 36–45.CrossRefGoogle Scholar
Jones, A. R. & Babinsky, H. 2011 Reynolds number effects on leading edge vortex development. Exp. Fluids 51 (1), 197–210.CrossRefGoogle Scholar
Jones, K. D. & Platzer, M. F. 1998 On the prediction of dynamic stall onset on airfoils in low speed flow. In Unsteady Aerodynamics and Aeroelasticity of Turbomachines (ed. Fransson, T. H.), pp. 797–812. Springer.CrossRefGoogle Scholar
Katz, J. 1981 A discrete vortex method for the non-steady separated flow over an airfoil. J. Fluid Mech. 102, 315–328.CrossRefGoogle Scholar
Katz, J. & Plotkin, A. 2001 Low-Speed Aerodynamics, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Lentink, D. & Dickinson, M. H. 2009 Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212 (16), 2705–2719.CrossRefGoogle ScholarPubMed
Lentink, D., Dickson, W. B., Van Leeuwen, J. L. & Dickinson, M. H. 2009 Leading-edge vortices elevate lift of autorotating plant seeds. Science 324 (5933), 1438–1440.CrossRefGoogle ScholarPubMed
Lian, Y. 2009 Parametric study of a pitching flat plate at low Reynolds numbers. AIAA Paper 2009-3688.CrossRefGoogle Scholar
Limacher, E., Morton, C. & Wood, D. 2016 On the trajectory of leading-edge vortices under the influence of coriolis acceleration. J. Fluid Mech. 800, R1.CrossRefGoogle Scholar
Limacher, E. & Rival, D. E. 2015 On the distribution of leading-edge vortex circulation in samara-like flight. J. Fluid Mech. 776, 316–333.CrossRefGoogle Scholar
Lorber, P. F., Carta, F. O. & Covinno, A. F. Jr., 1992 An oscillating three-dimensional wing experiment: compressibility, sweep, rate, waveform, and geometry effects on unsteady separation and dynamic stall. UTRC Tech. Rep. R92-958325-6. UTRC.Google Scholar
Lorber, P. F., Covino, A. F., Jr. & Carta, F. O. 1991 Dynamic stall experiments on a swept three-dimensional wing in compressible flow. AIAA Paper 91-1795.CrossRefGoogle Scholar
Maltby, R. L. 1968 The development of the slender delta concept. Aircraft Engng Aerosp. Technol. 40 (3), 12–17.CrossRefGoogle Scholar
Maxworthy, T. 1979 Experiments on the Weis-Fogh mechanism of lift generation by insects in hovering flight. Part 1. Dynamics of the ‘fling’. J. Fluid Mech. 93, 47–63.CrossRefGoogle Scholar
Maxworthy, T. 2007 The formation and maintenance of a leading-edge vortex during the forward motion of an animal wing. J. Fluid Mech. 587, 471–475.CrossRefGoogle Scholar
McCroskey, W. J., Carr, L. W. & McAlister, K. W. 1976 Dynamic stall experiments on oscillating airfoils. AIAA J. 14 (1), 57–63.CrossRefGoogle Scholar
McCroskey, W. J., McAlister, K., Carr, L. W., Pucci, S. L., Lambert, O. & Indergrand, L. R. F. 1981 Dynamic stall on advanced airfoil sections. J. Am. Helicopter Soc. 26, 40–50.CrossRefGoogle Scholar
McCroskey, W. J. & Pucci, S. L. 1982 Viscous-inviscid interaction on oscillating airfoils in subsonic flow. AIAA J. 20 (2), 167–174.CrossRefGoogle Scholar
McCullough, G. B. & Gault, D. E. 1951 Examples of three representative types of airfoil-section stall at low speed. NACA Tech. Rep. TN 2502. National Advisory Committee for Aeronautics.Google Scholar
Morris, W. J. & Rusak, Z. 2013 Stall onset on aerofoils a low to moderately high Reynolds number flows. J. Fluid Mech. 733, 439–472.CrossRefGoogle Scholar
Muijres, F. T., Johansson, L. C., Barfield, R., Wolf, M., Spedding, G. R. & Hedenström, A. 2008 Leading-edge vortex improves lift in slow-flying bats. Science 319 (5867), 1250–1253.CrossRefGoogle ScholarPubMed
Mulleners, K. & Raffel, M. 2012 The onset of dynamic stall revisited. Exp. Fluids 52, 779–793.CrossRefGoogle Scholar
Murua, J., Palacios, R. & Graham, J. M. R. 2012 Applications of the unsteady vortex-lattice method in aircraft aeroelasticity and flight dynamics. Prog. Aerosp. Sci. 55, 46–72.CrossRefGoogle Scholar
Ol, M. V. 2009 The high-frequency, high-amplitude pitch problem: airfoils, plates and wings. AIAA Paper 2009-3686.Google Scholar
Polhamus, E. C. 1966 A concept of the vortex lift of sharp-edge delta wings based on a leading-edge-suction analogy. NASA Tech. Rep. TN D-3767. National Aeronautics and Space Administration.Google Scholar
Polhamus, E. C. 1971 Prediction of vortex-lift characteristics by a leading-edge suction analogy. J. Aircraft 8 (4), 193–199.CrossRefGoogle Scholar
Ramesh, K., Gopalarathnam, A., Edwards, J. R., Ol, M. V. & Granlund, K. 2013 An unsteady airfoil theory applied to pitching motions validated against experiment and computation. Theor. Comput. Fluid Dyn. 27 (6), 843–864.CrossRefGoogle Scholar
Ramesh, K., Gopalarathnam, A., Granlund, K., Ol, M. V. & Edwards, J. R. 2014 Discrete-vortex method with novel shedding criterion for unsteady airfoil flows with intermittent leading-edge vortex shedding. J. Fluid Mech. 751, 500–538.CrossRefGoogle Scholar
Ramesh, K., Granlund, K., Ol, M. V., Gopalarathnam, A. & Edwards, J. R. 2017 Leading-edge flow criticality as a governing factor in leading-edge vortex initiation in unsteady airfoil flows. Theor. Comput. Fluid Dyn. 32 (2), 109–136.CrossRefGoogle Scholar
Rao, D. M. & Campbell, J. F. 1987 Vortical flow management techniques. Prog. Aerosp. Sci. 24 (3), 173–224.CrossRefGoogle Scholar
Schreck, S. & Robinson, M. 2005 Blade three-dimensional dynamic stall response to wind turbine operating condition. J. Solar Energy Engng 127 (4), 488–495.CrossRefGoogle Scholar
Schreck, S. J. & Helin, H. E. 1994 Unsteady vortex dynamics and surface pressure topologies on a finite pitching wing. J. Aircraft 31 (4), 899–907.CrossRefGoogle Scholar
Selig, M. S., Donovan, J. F. & Fraser, D. B. 1989 Airfoils at Low Speeds. Soartech 8. SoarTech Publications.Google Scholar
Spentzos, A., Barakos, G. N., Badcock, K. J., Richards, B. E., Coton, F. N. & Galbraith, R. A. M. 2007 Computational fluid dynamics study of three-dimensional dynamic stall of various planform shapes. J. Aircraft 44 (4), 1118–1128.CrossRefGoogle Scholar
Taylor, G. K., Nudds, R. L. & Thomas, A. L. 2003 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 425 (6959), 707–711.CrossRefGoogle Scholar
Venkata, S. K. & Jones, A. R. 2013 Leading-edge vortex structure over multiple revolutions of a rotating wing. J. Aircraft 50 (4), 1312–1316.CrossRefGoogle Scholar
Visbal, M., Yilmaz, T. O. & Rockwell, D. 2013 Three-dimensional vortex formation on a heaving low-aspect-ratio wing: computations and experiments. J. Fluids Struct. 38, 58–76.CrossRefGoogle Scholar
Visbal, M. R. & Gordnier, R. E. 1995 Pitch rate and pitch-axis location effects on vortex breakdown onset. J. Aircraft 32 (5), 929–935.CrossRefGoogle Scholar
Visbal, M. R. & Shang, J. S. 1989 Investigation of the flow structure around a rapidly pitching airfoil. AIAA J. 27 (8), 1044–1051.CrossRefGoogle Scholar
Walker, J. M., Helin, H. E. & Strickland, J. H. 1985 An experimental investigation of an airfoil undergoing large-amplitude pitching motions. AIAA J. 23 (8), 1141–1142.CrossRefGoogle Scholar
Wojcik, C. J. & Buchholz, J. H. J. 2014 Vorticity transport in the leading-edge vortex on a rotating blade. J. Fluid Mech. 743, 249–261.CrossRefGoogle Scholar
Wong, J. G. & Rival, D. E. 2015 Determining the relative stability of leading-edge vortices on nominally two-dimensional flapping profiles. J. Fluid Mech. 766, 611–625.CrossRefGoogle Scholar
Yilmaz, T. O. & Rockwell, D. 2012 Flow structure on finite-span wings due to pitch-up motion. J. Fluid Mech. 691, 518–545.CrossRefGoogle Scholar
Young, J., Lai, J. C. & Platzer, M. F. 2014 A review of progress and challenges in flapping foil power generation. Prog. Aerosp. Sci. 67, 2–28.CrossRefGoogle Scholar