Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T04:54:49.485Z Has data issue: false hasContentIssue false
  • English
  • Français

Free surface over a horizontal shear layer: vorticity generation and air entrainment mechanisms

Published online by Cambridge University Press:  26 January 2017

Matthieu A. André  and
Philippe M. Bardet
Matthieu A. André*
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, Washington, DC 20052, USA
Philippe M. Bardet*
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, Washington, DC 20052, USA
*
†Email addresses for correspondence: matandre@gwu.edu, bardet@gwu.edu
†Email addresses for correspondence: matandre@gwu.edu, bardet@gwu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Two air entrainment mechanisms driven by vortex instability are reported in the unstable relaxation of a horizontal shear layer below a free surface. This flow is experimentally investigated by means of planar laser-induced fluorescence (PLIF) and particle image velocimetry (PIV) coupled with surface profilometry. PLIF identifies counter-rotating vortex pairs (CRVP) emanating from the surface following the growth of high steepness two-dimensional millimetre-size waves for Reynolds and Weber numbers based on the momentum thickness of 177 to 222 and 7.59 to 13.9, respectively. High spatio-temporal resolution PIV reveals the role of surface-generated vorticity and flow separation in the highly curved trough of the waves on the injection of a CRVP. Air bubbles are entrapped in the wake of these CRVPs at Reynolds number above 190. PIV data and spanwise PLIF images show two initiation mechanisms: primary vortex instability modulating the spanwise location where the flow separates, resulting in the pinch off of an air ligament, and secondary vortex instability turning a CRVP into 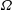$\unicode[STIX]{x1D6FA}$-shaped loops pulling the surface down. Instability wavelengths agree with linear stability analysis, and models for these new air entrainment mechanisms are proposed.

JFM classification

Drops and Bubbles: Drops and Bubbles Interfacial Flows (free surface): Interfacial Flows (free surface) Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 813 , 25 February 2017 , pp. 1007 - 1044
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agbaglah, G., Thoraval, M.-J., Thoroddsen, S. T., Zhang, L. V., Fezzaa, K. & Deegan, R. D. 2015 Drop impact into a deep pool: vortex shedding and jet formation. J. Fluid Mech. 764, R1.CrossRefGoogle Scholar
André, M. A. & Bardet, P. M. 2012 Experimental investigation of boundary layer instabilities on the free surface of non-turbulent jet. In ASME 2012 Fluids Engineering Division Summer Meeting collocated with the ASME 2012 Heat Transfer Summer Conference and the ASME 2012 10th International Conference on Nanochannels, Microchannels, and Minichannels, pp. 111–119.Google Scholar
André, M. A. & Bardet, P. M. 2014 Velocity field, surface profile and curvature resolution of steep and short free-surface waves. Exp. Fluids 55 (4), 1–19.Google Scholar
André, M. A. & Bardet, P. M. 2015a Experimental study of shear layer instability below a free surface. Phys. Fluids 27 (11), 112103.CrossRefGoogle Scholar
André, M. A. & Bardet, P. M. 2015b Interfacial shear stress measurement using high spatial resolution multiphase PIV. Exp. Fluids 56 (6), 1–18.CrossRefGoogle Scholar
Banerjee, P. P. & Korpel, A. 1982 Subharmonic generation by resonant three-wave interaction of deep-water capillary waves. Phys. Fluids 25 (11), 1938–1943.Google Scholar
Bardet, P. M., André, M. A. & Neal, D. R. 2013 Systematic timing errors in laser-based transit-time velocimetry. In 10th International Symposium on Particle Image Velocimetry – PIV13.Google Scholar
Bernal, L. P. & Kwon, J. T. 1989 Vortex ring dynamics at a free surface. Phys. Fluids A 1 (3), 449–451.Google Scholar
Biń, A. K. 1993 Gas entrainment by plunging liquid jets. Chem. Engng Sci. 48 (21), 3585–3630.Google Scholar
Brennen, C. E. 1970 Cavity surface wave patterns and general appearance. J. Fluid Mech. 44, 33–49.Google Scholar
Chanson, H. 1996 Air Bubble Entrainment in Free-Surface Turbulent Shear Flows. Academic.Google Scholar
Chanson, H. 2007 Bubbly flow structure in hydraulic jump. Eur. J. Mech. (B/Fluids) 26 (3), 367–384.CrossRefGoogle Scholar
Clift, R., Grace, J. R. & Weber, M. E. 2005 Bubbles, Drops, and Particles. Courier Corporation.Google Scholar
Crapper, G. D. 1957 An exact solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 2 (6), 532–540.Google Scholar
Crow, S. C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8 (12), 2172–2179.CrossRefGoogle Scholar
Dabiri, D. & Gharib, M. 1997 Experimental investigation of the vorticity generation within a spilling water wave. J. Fluid Mech. 330, 113–139.Google Scholar
Danckwerts, P. V. 1951 Significance of liquid-film coefficients in gas absoption. Ind. Engng Chem. 43 (6), 1460–1467.Google Scholar
Davies, J. T. & Driscoll, J. P. 1974 Eddies in free surfaces, simulated by pulses of water. Ind. Engng Chem. Fundam. 13 (2), 105–109.Google Scholar
Dommermuth, D. G. 1993 The laminar interactions of a pair of vortex tubes with a free surface. J. Fluid Mech. 246, 91–115.Google Scholar
Donelan, M. A. & Wanninkhof, R. 2002 Gas Transfer at Water Surfaces Concepts and Issues. American Geophysical Union.Google Scholar
Duncan, J. H., Qiao, H., Philomin, V. & Wenz, A 1999 Gentle spilling breakers: crest profile evolution. J. Fluid Mech. 379, 191–222.CrossRefGoogle Scholar
Faeth, G. M., Hsiang, L. P. & Wu, P. K. 1995 Structure and breakup properties of sprays. Intl J. Multiphase Flow 21, 99–127.CrossRefGoogle Scholar
Gharib, M. & Weigand, A. 1996 Experimental studies of vortex disconnection and connection at a free surface. J. Fluid Mech. 321, 59–86.Google Scholar
Green, S. I. 1995 Fluid Vortices: Fluid Mechanics and Its Applications. Kluwer Academic.CrossRefGoogle Scholar
Hammack, J. L. & Henderson, D. M. 1993 Resonant interactions among surface water waves. Annu. Rev. Fluid Mech. 25 (1), 55–97.CrossRefGoogle Scholar
Hecker, G. E. 1981 Model-prototype comparision of free surface vortices. J. Hydraul. Div. ASCE 107 (10), 1243–1259.Google Scholar
Hirsa, A. & Willmarth, W. W. 1994 Measurements of vortex pair interaction with a clean or contaminated free surface. J. Fluid Mech. 259, 25–45.CrossRefGoogle Scholar
Hoyt, J. W. & Taylor, J. J. 1977 Turbulence structure in a water jet discharging in air. Phys. Fluids 20 (10), 253–257.CrossRefGoogle Scholar
Iafrati, A. & Campana, E. F. 2005 Free-surface fluctuations behind microbreakers: space time behaviour and subsurface flow field. J. Fluid Mech. 529, 311–347.CrossRefGoogle Scholar
Itoh, K., Tsuji, Y. & Nakamura, H. 1999 Initial free surface instabilities on a high-speed water jet simulating a liquid-metal target. Fusion Technol. 36 (1), 69–84.Google Scholar
Jähne, B. & Haußecker, H. 1998 Air-water gas exchange. Annu. Rev. Fluid Mech. 30 (1), 443–468.Google Scholar
Kiger, K. T. & Duncan, J. H. 2012 Air-entrainment mechanisms in plunging jets and breaking waves. Annu. Rev. Fluid Mech. 44, 563–596.CrossRefGoogle Scholar
Klein, R., Majda, A. J. & Damodaran, K. 1995 Simplified equations for the interaction of nearly parallel vortex filaments. J. Fluid Mech. 288, 201–248.CrossRefGoogle Scholar
Koga, M. 1982 Bubble entrainment in breaking wind waves. Tellus 34 (5), 481–489.Google Scholar
Lin, C. C. 1966 The Theory of Hydrodynamic Stability. Cambridge University Press.Google Scholar
Lin, J. C. & Rockwell, D. 1995 Evolution of a quasi-steady breaking wave. J. Fluid Mech. 302, 29–44.Google Scholar
Longuet-Higgins, M. S. 1953 Mass transport in water waves. Phil. Trans. R. Soc. Lond. A 245 (903), 535–581.Google Scholar
Longuet-Higgins, M. S. 1992 Capillary rollers and bores. J. Fluid Mech. 240, 659–679.Google Scholar
Longuet-Higgins, M. S. 1994 Shear instability in spilling breakers. Proc. R. Soc. Lond. A 446, 399–409.Google Scholar
Longuet-Higgins, M. S. 1998 Instabilities of a horizontal shear flow with a free surface. J. Fluid Mech. 364, 147–162.Google Scholar
Lozano, M. M., Talu, E. & Longo, M. L. 2007 Dissolution of microbubbles generated in seawater obtained offshore: behavior and surface tension measurements. J. Geophys. Res. 112 (C12).CrossRefGoogle Scholar
Lugt, H. J. 1987 Local flow properties at a viscous free surface. Phys. Fluids 30, 3647.CrossRefGoogle Scholar
Lundgren, T. & Koumoutsakos, P. 1999 On the generation of vorticity at a free surface. J. Fluid Mech. 382, 351–366.CrossRefGoogle Scholar
Lundgren, T. S. 1989 A free surface vortex method with weak viscous effects. Mathematical Aspects of Vortex Dynamics vol. 1, pp. 68–79.Google Scholar
Madarame, H. & Chiba, T. 1990 Gas entrainment inception at the border of a flow-swollen liquid surface. Nucl. Engng Des. 120 (2), 193–201.Google Scholar
Marshall, J. S., Brancher, P. & Giovannini, A. 2001 Interaction of unequal anti-parallel vortex tubes. J. Fluid Mech. 446, 229–252.CrossRefGoogle Scholar
McLean, J. W. 1982 Instabilities of finite-amplitude water waves. J. Fluid Mech. 114, 315–330.Google Scholar
Mui, R. & Dommermuth, D. G. 1995 The vortical structure of parasitic capillary waves. Trans. ASME J. Fluids Engng 117 (3), 355–361.Google Scholar
Ohring, S. & Lugt, H. J. 1991 Interaction of a viscous vortex pair with a free surface. J. Fluid Mech. 227, 47–70.Google Scholar
Ortega, J. M., Bristol, R. L. & Savas, Ö. 2003 Experimental study of the instability of unequal-strength counter-rotating vortex pairs. J. Fluid Mech. 474, 35–84.Google Scholar
Osborne, T. J. & Stump, D. M. 2001 Capillary waves on a eulerian jet emerging from a channel. Phys. Fluids 13 (3), 616–623.Google Scholar
Perlin, M. & Schultz, W. W. 2000 Capillary effects on surface waves. Annu. Rev. Fluid Mech. 32 (1), 241–274.Google Scholar
Phillips, O. M. 1960 On the dynamics of unsteady gravity waves of finite amplitude. Part 1. The elementary interactions. J. Fluid Mech. 9 (02), 193–217.Google Scholar
Ponstein, J. 1959 Instability of rotating cylindrical jets. Appl. Sci. Res. A 8 (1), 425–456.Google Scholar
Portillo, J. E., Collicott, S. H. & Blaisdell, G. A. 2011 Measurements of axial instability waves in the near exit region of a high speed liquid jet. Phys. Fluids 23 (12), 124105.Google Scholar
Qiao, H. & Duncan, J. H. 2001 Gentle spilling breakers: crest flow-field evolution. J. Fluid Mech. 439, 57–85.Google Scholar
Rood, E. P. 1995 Vorticity interactions with a free surface. In Fluid Vortices, pp. 687–730. Springer.Google Scholar
Sajjadi, S. G. 2002 Vorticity generated by pure capillary waves. J. Fluid Mech. 459, 277–288.Google Scholar
Sarpkaya, T. & Henderson, D. O. Jr 1985 Free surface scars and striations due to trailing vortices generated by a submerged lifting surface. In AIAA Aerospace Sciences Meeting, vol. 1.Google Scholar
Sarpkaya, T. & Suthon, P. 1991 Interaction of a vortex couple with a free surface. Exp. Fluids 11 (4), 205–217.Google Scholar
Saylor, J. R. & Handler, R. A. 1997 Gas transport across an air/water interface populated with capillary waves. Phys. Fluids 9 (9), 2529–2541.Google Scholar
Sébilleau, J., Limat, L. & Eggers, J. 2009 Flow separation from a stationary meniscus. J. Fluid Mech. 633, 137–145.Google Scholar
Simmons, W. F. 1969 A variational method for weak resonant wave interactions. Proc. R. Soc. Lond. A 309, 551–577.Google Scholar
Terrill, E. J. & Taylor, G. RL. 2015 Entrainment of air at the transoms of full-scale surface ships. J. Ship Res. 59 (1), 49–65.Google Scholar
Willert, C. E. & Gharib, M. 1997 The interaction of spatially modulated vortex pairs with free surfaces. J. Fluid Mech. 345, 227–250.Google Scholar
Yoon, S. S. & Heister, S. D. 2004 A nonlinear atomization model based on a boundary layer instability mechanism. Phys. Fluids 16 (1), 47–61.CrossRefGoogle Scholar
Yu, D. & Tryggvason, G. 1990 The free-surface signature of unsteady, two-dimensional vortex flows. J. Fluid Mech. 218, 547–572.Google Scholar
Zhang, C., Shen, L. & Yue, D. 1999 The mechanism of vortex connection at a free surface. J. Fluid Mech. 384, 207–241.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar