Article contents
General exotic capillary tubes
Published online by Cambridge University Press: 17 December 2019
Abstract
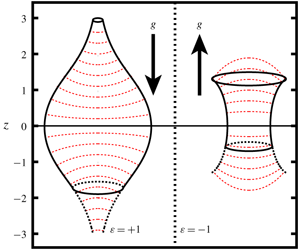
The general exotic capillary tube is a non-uniform capillary tube which permits an entire continuum of equilibrium menisci if applying a pressure  $p=-\unicode[STIX]{x1D700}z$ at the tube inlet. The shapes of general exotic capillary tubes under positive and negative loads are determined mathematically. Lowering the pressure at the tube inlet slightly from the value
$p=-\unicode[STIX]{x1D700}z$ at the tube inlet. The shapes of general exotic capillary tubes under positive and negative loads are determined mathematically. Lowering the pressure at the tube inlet slightly from the value  $p=-\unicode[STIX]{x1D700}z$ causes the tube to completely drain out, while raising the pressure slightly forces the tube to fill up, which implies that the general exotic capillary tube is sensitive to pressure. The general exotic capillary tube is also related to meniscus stability. It is found that the boundary parameters
$p=-\unicode[STIX]{x1D700}z$ causes the tube to completely drain out, while raising the pressure slightly forces the tube to fill up, which implies that the general exotic capillary tube is sensitive to pressure. The general exotic capillary tube is also related to meniscus stability. It is found that the boundary parameters  $\unicode[STIX]{x1D712}_{1}$ of general exotic cylinders with arbitrary contact angle are equal to the critical values
$\unicode[STIX]{x1D712}_{1}$ of general exotic cylinders with arbitrary contact angle are equal to the critical values  $\unicode[STIX]{x1D712}_{1}^{\ast }$ for determining the meniscus stability. Then, a convenient alternative to solving the Jacobi equation for determining
$\unicode[STIX]{x1D712}_{1}^{\ast }$ for determining the meniscus stability. Then, a convenient alternative to solving the Jacobi equation for determining  $\unicode[STIX]{x1D712}_{1}^{\ast }$ is proposed based on the ‘exotic’ property.
$\unicode[STIX]{x1D712}_{1}^{\ast }$ is proposed based on the ‘exotic’ property.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 6
- Cited by


