Article contents
Geostrophic adjustment in a closed basin with islands
Published online by Cambridge University Press: 05 December 2013
Abstract
We consider the geostrophic adjustment of a density-stratified fluid in a basin of constant depth on an 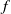 $f$ -plane in the context of linearized theory. For a single vertical mode, the equations are equivalent to those for a linearized shallow-water theory for a homogeneous fluid. Associated with any initial state there is a unique steady geostrophically adjusted component of the flow compatible with the initial conditions. This steady component gives the time average of the flow and is analogous to the adjusted flow in an unbounded domain without islands. The remainder of the response consists of superinertial Poincaré and subinertial Kelvin wave modes and expressions for the energy partition between the modes in arbitrary basins again follow directly from the initial conditions. The solution for an arbitrary initial density distribution released from rest in a circular domain is found in closed form. When the Rossby radius is much smaller than the basin radius, appropriate for the baroclinic modes, the interior adjusted solution is close to that of the initial state, except for small-amplitude trapped Poincaré waves, while Kelvin waves propagate around the boundaries, carrying, without change of form, the deviation of the initial height field from its average.
$f$ -plane in the context of linearized theory. For a single vertical mode, the equations are equivalent to those for a linearized shallow-water theory for a homogeneous fluid. Associated with any initial state there is a unique steady geostrophically adjusted component of the flow compatible with the initial conditions. This steady component gives the time average of the flow and is analogous to the adjusted flow in an unbounded domain without islands. The remainder of the response consists of superinertial Poincaré and subinertial Kelvin wave modes and expressions for the energy partition between the modes in arbitrary basins again follow directly from the initial conditions. The solution for an arbitrary initial density distribution released from rest in a circular domain is found in closed form. When the Rossby radius is much smaller than the basin radius, appropriate for the baroclinic modes, the interior adjusted solution is close to that of the initial state, except for small-amplitude trapped Poincaré waves, while Kelvin waves propagate around the boundaries, carrying, without change of form, the deviation of the initial height field from its average.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 2
- Cited by

