Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T06:48:10.842Z Has data issue: false hasContentIssue false
  • English
  • Français

The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes model with a μ(I)-rheology

Published online by Cambridge University Press:  27 September 2011

P.-Y. Lagrée ,
L. Staron  and
S. Popinet
P.-Y. Lagrée*
Affiliation:
CNRS and UPMC Université Paris 06, UMR 7190, Institut Jean Le Rond d’Alembert, Boîte 162, F-75005 Paris, France
L. Staron
Affiliation:
CNRS and UPMC Université Paris 06, UMR 7190, Institut Jean Le Rond d’Alembert, Boîte 162, F-75005 Paris, France
S. Popinet
Affiliation:
CNRS and UPMC Université Paris 06, UMR 7190, Institut Jean Le Rond d’Alembert, Boîte 162, F-75005 Paris, France National Institute of Water and Atmospheric Research, PO Box 14-901 Kilbirnie, Wellington, New Zealand
*
†Email address for correspondence: pierre-yves.lagree@upmc.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

There is a large amount of experimental and numerical work dealing with dry granular flows (such as sand, glass beads, etc.) that supports the so-called 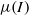-rheology. The reliability of the 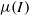-rheology in the case of complex transient flows is not fully ascertained, however. From this perspective, the granular column collapse experiment provides an interesting benchmark. In this paper we implement the 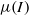-rheology in a Navier–Stokes solver (Gerris) and compare the resulting solutions with both analytical solutions and two-dimensional contact dynamics discrete simulations. In a first series of simulations, we check the numerical model in the case of a steady infinite two-dimensional granular layer avalanching on an inclined plane. A second layer of Newtonian fluid is then added over the granular layer in order to recover a close approximation of a free-surface condition. Comparisons with analytical and semi-analytical solutions provide conclusive validation of the numerical implementation of the 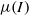-rheology. In a second part, we simulate the unsteady two-dimensional collapse of granular columns over a wide range of aspect ratios. Systematic comparisons with discrete two-dimensional contact dynamics simulations show good agreement between the two methods for the inner deformations and the time evolution of the shape during most of the flow, while a systematic underestimation of the final run-out is observed. The experimental scalings of spreading of the column as a function of the aspect ratio available from the literature are also recovered. A discussion follows on the performances of other rheologies, and on the sensitivity of the simulations to the parameters of the 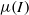-rheology.

JFM classification

Granular media: Granular media Non-Newtonian Flows: Non-Newtonian Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 686 , 10 November 2011 , pp. 378 - 408
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ancey, C., Coussot, P. & Evesque, P. 1999 A theoretical framework for granular suspensions in a steady simple shear flow. J. Rheol. 43, 1673–1699.CrossRefGoogle Scholar
2. Aranson, I. S. & Tsimring, L. S. 2001 Continuum description of avalanches in granular media. Phys. Rev. E 64, 020301.CrossRefGoogle ScholarPubMed
3. Bagnold, R. G. 1954 Experiments of gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. Lond. A 255, 49.Google Scholar
4. Bagué, A., Fuster, D., Popinet, S., Scardovelli, R. & Zaleski, S. 2010 Instability growth rate of two-phase mixing layers from a linear eigenvalue problem and an initial value problem. Phys. Fluids 22, 092104.CrossRefGoogle Scholar
5. Balmforth, N. J. & Kerswell, R. R. 2005 Granular collapse in two dimensions. J. Fluid Mech. 538, 399–428.CrossRefGoogle Scholar
6. Bell, J. B., Colella, P. & Glaz, H. M. A second-order projection method for the incompressible Navier–Stokes equations. J. Comput. Phys. 85, 257–283.CrossRefGoogle Scholar
7. Bouchut, F., Fernández-Nieto, E. D., Mangeney, A. & Lagrée, P.-Y. 2008 On new erosion models of Savage–Hutter type for avalanches. Acta Mechanica 199 (1–4), 181–208.CrossRefGoogle Scholar
8. Cassar, C., Nicolas, M. & Pouliquen, O. 2005 Submarine granular flows down inclined planes. Phys. Fluids 17, 103301.CrossRefGoogle Scholar
9. Cawthorn, C. J. 2011 Several applications of a model for dense granular flows. PhD thesis, University of Cambridge.Google Scholar
10. Chauchat, J. & Médale, M. 2010 A three-dimensional numerical model for incompresible two-phase flow of a granular bed submitted to a laminar shearing flow. Comput. Meth. Appl. Mech. Engng 199, 439–449.CrossRefGoogle Scholar
11. Courrech du Pont, S., Gondret, P., Perrin, B. & Rabaud, M. 2003 Wall effects on granular heap stability. Europhys. Lett. 61 (4), 492–498.CrossRefGoogle Scholar
12. Crosta, G. B., Imposimato, S. & Roddeman, D. 2009 Numerical modelling of 2-D granular step collapse on erodible and nonerodible surface. J. Geophys. Res. 114, F03020.CrossRefGoogle Scholar
13. da Cruz, F. 2004 Écoulements de grains secs: frottement et blocage. Thèse de l’École Nationale des Ponts et Chaussées http://pastel.paristech.org/archive/946/.Google Scholar
14. da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys. Rev. E 72, 021309.CrossRefGoogle ScholarPubMed
15. Daerr, A. & Douady, S. 1999 Sensitivity of granular surface flows to preparation. Europhys. Lett. 47 (3), 324–330.CrossRefGoogle Scholar
16. Davies, T., McSaveney, M. & Kelfoun, K. 2010 Runout of the Socompa volcanic debris avalanche, Chile: a mechanical explanation for low basal shear resistance. Bull. Volcanol. 72 (8), 933–944.CrossRefGoogle Scholar
17. Doyle, E. E., Huppert, H. E., Lube, G., Mader, H. M. & Sparks, R. S. J. 2007 Static and flowing regions in granular collapses down channels: insights from a sedimenting shallow water model. Phys. Fluids 19, 106601.CrossRefGoogle Scholar
18. Dufour, F. & Pijaudier-Cabot, G. 2005 Numerical modelling of concrete flow. Homogeneous approach. Intl J. Numer. Anal. Meth. Geomech. 29, 395–416.CrossRefGoogle Scholar
19. Fuster, D., Agbaglah, G., Josserand, C., Popinet, S. & Zaleski, S. 2009a Numerical simulation of droplets, bubbles and waves: state of the art. Fluid Dyn. Res. 41, 065001.CrossRefGoogle Scholar
20. Fuster, D., Bagué, A., Boeck, T., Le Moyne, L., Leboissetier, A., Popinet, S., Ray, P., Scardovelli, R. & Zaleski, S. 2009b Simulation of primary atomization with an octree adaptive mesh refinement and VOF method. Intl J. Multiphase Flow 35 (6), 550–565.CrossRefGoogle Scholar
21. GdR MiDi, 2004 On dense granular flows. Eur. Phys. J. E 14, 341–365.CrossRefGoogle Scholar
22. Hatano, T. J. 2007 Power-law friction in closely packed granular materials. Phys. Rev. E 75, 060301.CrossRefGoogle ScholarPubMed
23. Hogg, A. J. 2007 Two-dimensional granular slumps down slopes. Phys. Fluids 19, 093301.CrossRefGoogle Scholar
24. Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 130, 187–202.CrossRefGoogle Scholar
25. Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.CrossRefGoogle Scholar
26. Jop, P., Forterre, Y. & Pouliquen, O. 2006 A rheology for dense granular flows. Nature 441, 727–730.CrossRefGoogle Scholar
27. Josserand, C., Lagrée, P.-Y. & Lhuillier, D. 2004 Stationary shear flows of dense granular materials: a tentative continuum modelling. Eur. Phys. J. E 14, 127.CrossRefGoogle ScholarPubMed
28. Josserand, C., Lagrée, P.-Y. & Lhuillier, D. 2006 Granular pressure and the thickness of a layer jamming on a rough incline. Europhys. Lett. 73 (3), 363–369.CrossRefGoogle Scholar
29. Josserand, C, Lagrée, P.-Y., Lhuillier, D., Popinet, S., Ray, P. & Staron, L. 2009 The spreading of a granular column from a Bingham point of view. In Powders and Grains, AIP Conference Proceedings, vol. 000, pp. 631–634. American Institute of Physics.CrossRefGoogle Scholar
30. Kelfoun, K., Samaniego, P., Palacios, P. & Barba, D. 2009 Testing the suitability of frictional behaviour for pyroclastic flow simulation by comparison with a well-constrained eruption at Tungurahua volcano (Ecuador). Bull. Volcanol. 71 (9), 1057–1075.CrossRefGoogle Scholar
31. Kerswell, R. R. 2005 Dam break with Coulomb friction: a model for granular slumping? Phys. Fluids 17, 057101.CrossRefGoogle Scholar
32. Lacaze, L. & Kerswell, R. R. 2009 Axisymmetric granular collapse: a transient three-dimensional flow test of viscoplasticity. Phys. Rev. Lett. 102, 108305.CrossRefGoogle ScholarPubMed
33. Lacaze, L., Phillips, J. C. & Kerswell, R. R. 2008 Planar collapse of a granular column: experiments and discrete element simulations. Phys. Fluids 20, 063302.CrossRefGoogle Scholar
34. Lagrée, P.-Y. 2010Bagnold flow of a granular material: http://gerris.dalembert.upmc.fr/gerris/tests/tests/poiseuille.html#toc11.Google Scholar
35. Lajeunesse, E., Mangeney-Castelneau, A. & Vilotte, J.-P. 2004 Spreading of a granular mass on an horizontal plane. Phys. Fluids 16, 2371–2381.CrossRefGoogle Scholar
36. Lajeunesse, E., Monnier, J. B. & Homsy, G. M. 2005 Granular slumping on a horizontal surface. Phys. Fluids 17, 103302.CrossRefGoogle Scholar
37. Lajeunesse, E., Quantin, C., Allemand, P. & Delacourt, C. 2006 New insights on the runout of large landslides in the Valles–Marineris canyons. Mars Geophys. Res. Lett. 33, L04403.CrossRefGoogle Scholar
38. Larrieu, E., Staron, L. & Hinch, E. J. 2006 Raining into shallow water as a description of the collapse of a column of grains. J. Fluid Mech. 554, 259–270.CrossRefGoogle Scholar
39. Lube, G., Huppert, H. E., Sparks, R. S. J. & Hallworth, M. A. 2004 Axisymmetric collapses of granular columns. J. Fluid Mech. 508, 175–199.CrossRefGoogle Scholar
40. Lube, G., Huppert, H. E., Sparks, R. S. J. & Freundt, A. 2005 Collapses of two-dimensional granular columns. Phys. Rev. E 72, 041301.CrossRefGoogle ScholarPubMed
41. Mangeney, A., Roche, O., Hungr, O., Mangold, X. X. X., Faccanoni, G. & Lucas, A. 2010 Erosion and mobility in granular collapse over sloping beds. J. Geophys. Res. 115, F03040.CrossRefGoogle Scholar
42. Mangeney-Castelnau, A., Bouchut, F., Vilotte, J. P., Lajeunesse, E., Aubertin, A. & Pirulli, M. 2005 On the use of Saint Venant equations to simulate the spreading of a granular mass. J. Geophys. Res. 110, B09103.CrossRefGoogle Scholar
43. Mills, P., Loggia, D. & Tixier, M. 1999 Model for a stationnary dense granular flow along an inclined wall. Europhys. Lett. 45 (6), 733–738.CrossRefGoogle Scholar
44. Moreau, J.-J. 1994 Some numerical methods in multibody dynamics: application to granular materials. Eur. J. Mech. A 4, 93–114.Google Scholar
45. Nichol, K., Zanin, A., Bastien, R., Wandersman, E. & van Hecke, M. 2010 Flow-induced agitations create a granular fluid. Phys. Rev. Lett. 104, 078302.CrossRefGoogle ScholarPubMed
46. Pailha, M. & Pouliquen, O. 2009 A two-phase flow description of the initiation of underwater granular avalanches. J. Fluid Mech. 633, 115–135.CrossRefGoogle Scholar
47. Pomeau, Y. 2002 Recent progress in the moving contact line problem: a review. C. R. Acad. Sci. Paris 330, 207–222.Google Scholar
48. Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190 (2), 572–600.CrossRefGoogle Scholar
49. Popinet, S. 2005 Creeping Couette flow of generalised Newtonian fluids: http://gerris.dalembert.upmc.fr/gerris/tests/tests/couette.html.Google Scholar
50. Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228, 5838–5866.CrossRefGoogle Scholar
51. Popinet, S. 2011 Collapse of a column of grains: http://gerris.dalembert.upmc.fr/gerris/wiki/index.php/Examples.Google Scholar
52. Pouliquen, O. 1999 On the shape of granular fronts down rough inclined planes. Phys. Fluids 11 (7), 1956–1958.CrossRefGoogle Scholar
53. Pouliquen, O. & Forterre, Y. 2009 A non-local rheology for dense granular flows. Phil. Trans. R. Soc. A 367, 5091–5107.CrossRefGoogle ScholarPubMed
54. Pouliquen, O. & Forterre, Y. 2002 Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane. J. Fluid Mech. 453, 133–151.CrossRefGoogle Scholar
55. Rondon, L., Pouliquen, O. & Aussillous, P. 2011 Granular collapse in a fluid: role of the initial volume fraction. Phys. Fluids 23, 073301.CrossRefGoogle Scholar
56. Savage, S. B. 1979 Gravity flow of cohesionless granular materials in chutes and channels. J. Fluid Mech. 92, 53–96.CrossRefGoogle Scholar
57. Savage, S. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.CrossRefGoogle Scholar
58. Schlichting, H. 1987 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
59. Staron, L. & Hinch, E. J. 2005 Study of the collapse of granular columns using two-dimensional discrete-grain simulation. J. Fluid Mech. 545, 1–27.CrossRefGoogle Scholar
60. Staron, L. & Hinch, E. J. 2007 The spreading of a granular mass: role of grain properties and initial conditions. Granular Matter 9, 205–217.CrossRefGoogle Scholar
61. Staron, L., Lagrée, P.-Y., Josserand, C. & Lhuillier, D. 2010 Flow and jamming of two-dimensional granular bed: towards a non-local rheology? Phys. Fluids 22, 113303.CrossRefGoogle Scholar
62. Vola, D., Babik, F. & Latché, J.-C. 2004 On a numerical strategy to compute gravity currents of non-Newtonian fluids. J. Comput. Phys. 201 (2), 397–420.CrossRefGoogle Scholar
63. Zenit, R. 2005 Computer simulations of the collapse of a granular column. Phys. Fluids 17, 031703.CrossRefGoogle Scholar