Article contents
Kinetic energy transport in Rayleigh–Bénard convection
Published online by Cambridge University Press: 22 May 2015
Abstract
The kinetic energy balance in Rayleigh–Bénard convection is investigated by means of direct numerical simulations for the Prandtl number range 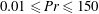 $0.01\leqslant \mathit{Pr}\leqslant 150$ and for fixed Rayleigh number
$0.01\leqslant \mathit{Pr}\leqslant 150$ and for fixed Rayleigh number 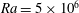 $\mathit{Ra}=5\times 10^{6}$. The kinetic energy balance is divided into a dissipation, a production and a flux term. We discuss the profiles of all the terms and find that the different contributions to the energy balance can be spatially separated into regions where kinetic energy is produced and where kinetic energy is dissipated. By analysing the Prandtl number dependence of the kinetic energy balance, we show that the height dependence of the mean viscous dissipation is closely related to the flux of kinetic energy. We show that the flux of kinetic energy can be divided into four additive contributions, each representing a different elementary physical process (advection, buoyancy, normal viscous stresses and viscous shear stresses). The behaviour of these individual flux contributions is found to be surprisingly rich and exhibits a pronounced Prandtl number dependence. Different flux contributions dominate the kinetic energy transport at different depths, such that a comprehensive discussion requires a decomposition of the domain into a considerable number of sublayers. On a less detailed level, our results reveal that advective kinetic energy fluxes play a key role in balancing the near-wall dissipation at low Prandtl number, whereas normal viscous stresses are particularly important at high Prandtl number. Finally, our work reveals that classical velocity boundary layers are deeply connected to the kinetic energy transport, but fail to correctly represent regions of enhanced viscous dissipation.
$\mathit{Ra}=5\times 10^{6}$. The kinetic energy balance is divided into a dissipation, a production and a flux term. We discuss the profiles of all the terms and find that the different contributions to the energy balance can be spatially separated into regions where kinetic energy is produced and where kinetic energy is dissipated. By analysing the Prandtl number dependence of the kinetic energy balance, we show that the height dependence of the mean viscous dissipation is closely related to the flux of kinetic energy. We show that the flux of kinetic energy can be divided into four additive contributions, each representing a different elementary physical process (advection, buoyancy, normal viscous stresses and viscous shear stresses). The behaviour of these individual flux contributions is found to be surprisingly rich and exhibits a pronounced Prandtl number dependence. Different flux contributions dominate the kinetic energy transport at different depths, such that a comprehensive discussion requires a decomposition of the domain into a considerable number of sublayers. On a less detailed level, our results reveal that advective kinetic energy fluxes play a key role in balancing the near-wall dissipation at low Prandtl number, whereas normal viscous stresses are particularly important at high Prandtl number. Finally, our work reveals that classical velocity boundary layers are deeply connected to the kinetic energy transport, but fail to correctly represent regions of enhanced viscous dissipation.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 16
- Cited by



