Article contents
Layer formation in sedimentary fingering convection
Published online by Cambridge University Press: 07 March 2017
Abstract
When particles settle through a stable temperature or salinity gradient they can drive an instability known as sedimentary fingering convection. This phenomenon is thought to occur beneath sediment-rich river plumes in lakes and oceans, in the context of marine snow where decaying organic materials serve as the suspended particles or in the atmosphere in the presence of aerosols or volcanic ash. Laboratory experiments of Houk & Green (Deep-Sea Res., vol. 20, 1973, pp. 757–761) and Green (Sedimentology, vol. 34(2), 1987, pp. 319–331) have shown sedimentary fingering convection to be similar to the more commonly known thermohaline fingering convection in many ways. Here, we study the phenomenon using three-dimensional direct numerical simulations. We find evidence for layer formation in sedimentary fingering convection in regions of parameter space where it does not occur for non-sedimentary systems. This is due to two complementary effects. Sedimentation affects the turbulent fluxes and broadens the region of parameter space unstable to the 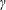 $\unicode[STIX]{x1D6FE}$-instability (Radko, J. Fluid Mech., vol. 497, 2003, pp. 365–380) to include systems at larger density ratios. It also gives rise to a new layering instability that exists in
$\unicode[STIX]{x1D6FE}$-instability (Radko, J. Fluid Mech., vol. 497, 2003, pp. 365–380) to include systems at larger density ratios. It also gives rise to a new layering instability that exists in  $\unicode[STIX]{x1D6FE}$-stable regimes. The former is likely quite ubiquitous in geophysical systems for sufficiently large settling velocities, while the latter probably grows too slowly to be relevant, at least in the context of sediments in water.
$\unicode[STIX]{x1D6FE}$-stable regimes. The former is likely quite ubiquitous in geophysical systems for sufficiently large settling velocities, while the latter probably grows too slowly to be relevant, at least in the context of sediments in water.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 15
- Cited by



