Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T05:28:37.961Z Has data issue: false hasContentIssue false
  • English
  • Français

Libration-driven multipolar instabilities

Published online by Cambridge University Press:  02 January 2014

D. Cébron ,
S. Vantieghem  and
W. Herreman
D. Cébron*
Affiliation:
Institut für Geophysik, Sonneggstrasse 5, ETH Zürich, CH-8092 Zürich, Switzerland
S. Vantieghem
Affiliation:
Institut für Geophysik, Sonneggstrasse 5, ETH Zürich, CH-8092 Zürich, Switzerland
W. Herreman
Affiliation:
Université de Paris-Sud (LIMSI-CNRS), BP 133, F-91403 Orsay CEDEX, France
*
†Email address for correspondence: dcebron@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider rotating flows in non-axisymmetric enclosures that are driven by libration, i.e. by a small periodic modulation of the rotation rate. Thanks to its simplicity, this model is relevant to various contexts, from industrial containers (with small oscillations of the rotation rate) to fluid layers of terrestrial planets (with length-of-day variations). Assuming a multipolar $n$-fold boundary deformation, we first obtain the two-dimensional basic flow. We then perform a short-wavelength local stability analysis of the basic flow, showing that an instability may occur in three dimensions. We christen it the libration-driven multipolar instability (LDMI). The growth rates of the LDMI are computed by a Floquet analysis in a systematic way, and compared to analytical expressions obtained by perturbation methods. We then focus on the simplest geometry allowing the LDMI, a librating deformed cylinder. To take into account viscous and confinement effects, we perform a global stability analysis, which shows that the LDMI results from a parametric resonance of inertial modes. Performing numerical simulations of this librating cylinder, we confirm that the basic flow is indeed established and report the first numerical evidence of the LDMI. Numerical results, in excellent agreement with the stability results, are used to explore the nonlinear regime of the instability (amplitude and viscous dissipation of the driven flow). We finally provide an example of LDMI in a deformed spherical container to show that the instability mechanism is generic. Our results show that the previously studied libration-driven elliptical instability simply corresponds to the particular case 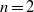$n= 2$ of a wider class of instabilities. Summarizing, this work shows that any oscillating non-axisymmetric container in rotation may excite intermittent, space-filling LDMI flows, and this instability should thus be easy to observe experimentally.

JFM classification

Instability: Parametric instability Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 739 , 25 January 2014 , pp. 502 - 543
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions, 5th edn. Dover.Google Scholar
Aldridge, K. D. 1967 An experimental study of axisymmetric inertial oscillations of a rotating liquid sphere. PhD thesis, University of Toronto, Canada.Google Scholar
Aldridge, K. D. 1975 Inertial waves and Earth’s outer core. Geophys. J. R. Astron. Soc. 42 (2), 337–345.Google Scholar
Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37 (2), 307–323.Google Scholar
Bayly, B. J. 1986 Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57 (17), 2160–2163.Google Scholar
Bayly, B. J., Holm, D. D. & Lifschitz, A. 1996 Three-dimensional stability of elliptical vortex columns in external strain flows. Phil. Trans. R. Soc. Lond. A 354 (1709), 895–926.Google Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory, vol. 1, Springer.Google Scholar
Busse, F. H. 2010a Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512.Google Scholar
Busse, F. H. 2010b Zonal flow induced by longitudinal librations of a rotating cylindrical cavity. Physica D: Nonlinear Phenom. 240 (2), 208–211.CrossRefGoogle Scholar
Calkins, M. A., Noir, J., Eldredge, J. D. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22, 086602.Google Scholar
Cambon, C., Benoit, J. P., Shao, L. & Jacquin, L. 1994 Stability analysis and large-eddy simulation of rotating turbulence with organized eddies. J. Fluid Mech. 278, 175–200.Google Scholar
Cambon, C., Teissedre, C. & Jeandel, D. 1985 Étude d’effets couplés de déformation et de rotation sur une turbulence homogène. J Méc. Théor. Appl. 4 (5), 629–657.Google Scholar
Cébron, D., Le Bars, M., Leontini, J., Maubert, P. & Le Gal, P. 2010a A systematic numerical study of the tidal instability in a rotating triaxial ellipsoid. Phys. Earth Planet. Inter. 182, 119–128.Google Scholar
Cébron, D., Le Bars, M., Maubert, P. & Le Gal, P. 2012a Magnetohydrodynamic simulations of the elliptical instability in triaxial ellipsoids. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 524–546.Google Scholar
Cébron, D., Le Bars, M. & Meunier, P. 2010b Tilt-over mode in a precessing triaxial ellipsoid. Phys. Fluids 22, 116601.Google Scholar
Cébron, D., Le Bars, M., Moutou, C. & Le Gal, P. 2012b Elliptical instability in terrestrial planets and moons. Astron. Astrophys. 539 (A78), 1–16.Google Scholar
Cébron, D., Le Bars, M., Noir, J. & Aurnou, J. M. 2012c Libration driven instability. Phys. Fluids 24 (6), 061703.Google Scholar
Cébron, D., Maubert, P. & Le Bars, M. 2010c Tidal instability in a rotating and differentially heated ellipsoidal shell. Geophys. J. Intl 182, 1311–1318.Google Scholar
Comstock, R. L. & Bills, B. G. 2003 A solar system survey of forced librations in longitude. J. Geophys. Res. 108 (E9), 5100 , 1–13.Google Scholar
Craik, A. D. D. & Criminale, W. O. 1986 Evolution of wavelike disturbances in shear flows: a class of exact solutions of the Navier–Stokes equations. Proc. R. Soc. Lond. A 406 (1830), 13–26.Google Scholar
Eckart, C. 1960 Hydrodynamics of Atmospheres and Oceans. Pergamon.Google Scholar
Eloy, C. & Le Dizès, S. 2001 Stability of the Rankine vortex in a multipolar strain field. Phys. Fluids 13, 660–676.CrossRefGoogle Scholar
Eloy, C., Le Gal, P. & Le Dizès, S. 2000 Experimental study of the multipolar vortex instability. Phys. Rev. Lett. 85 (16), 3400–3403.Google Scholar
Eloy, C., Le Gal, P. & Le Dizès, S. 2003 Elliptic and triangular instabilities in rotating cylinders. J. Fluid Mech. 476, 357–388.Google Scholar
Friedlander, S. & Vishik, M. M. 1991 Instability criteria for the flow of an inviscid incompressible fluid. Phys. Rev. Lett. 66 (17), 2204–2206.Google Scholar
Gledzer, E. B. & Ponomarev, V. M. 1992 Instability of bounded flows with elliptical streamlines. J. Fluid Mech. 240 (1), 1–30.Google Scholar
Guimbard, D., Le Dizès, S., Le Bars, M., Le Gal, P. & Leblanc, S. 2010 Elliptic instability of a stratified fluid in a rotating cylinder. J. Fluid Mech. 660, 240–257.Google Scholar
Ham, F., Mattsson, K. & Iaccarino, G. 2006 Accurate and stable finite volume operators for unstructured flow solvers. In Annual Research Briefs. Center for Turbulence Research, Stanford University, USA.Google Scholar
Henson, V. E. & Meier Yang, U. 2000 BoomerAMG: a parallel algebraic multigrid solver and preconditioner. Appl. Numer. Maths 41, 155–177.Google Scholar
Herreman, W., Cebron, D., Le Dizès, S. & Le Gal, P. 2010 Elliptical instability in rotating cylinders: liquid metal experiments under imposed magnetic field. J. Fluid Mech. 661, 130–158.Google Scholar
Herreman, W., Le Bars, M. & Le Gal, P. 2009 On the effects of an imposed magnetic field on the elliptical instability in rotating spheroids. Phys. Fluids 21, 046602.Google Scholar
Kerswell, R. R. 1993a Elliptical instabilities of stratified, hydromagnetic waves. Geophys. Astrophys. Fluid Dyn. 71 (1), 105–143.Google Scholar
Kerswell, R. R. 1993b The instability of precessing flow. Geophys. Astrophys. Fluid Dyn. 72 (1), 107–144.Google Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34 (1), 83–113.Google Scholar
Kerswell, R. R. & Barenghi, C. F. 1995 On the viscous decay rates of inertial waves in a rotating circular cylinder. J. Fluid Mech. 285, 203–214.CrossRefGoogle Scholar
Kerswell, R. R. & Malkus, W. V. R. 1998 Tidal instability as the source for Io’s magnetic signature. Geophys. Res. Lett. 25 (5), 603–606.Google Scholar
Kevorkian, J. & Cole, J. D. 1996 Multiple Scale and Singular Perturbation Methods, vol. 114, Springer.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to the incompressible Navier–Stokes equation. J. Comput. Phys. 59, 308–323.Google Scholar
Lacaze, L., Le Gal, P. & Le Dizès, S. 2004 Elliptical instability in a rotating spheroid. J. Fluid Mech. 505, 1–22.Google Scholar
Lacaze, L., Le Gal, P. & Le Dizès, S. 2005 Elliptical instability of the flow in a rotating shell. Phys. Earth Planet. Inter. 151 (3–4), 194–205.Google Scholar
Lagrange, R., Meunier, P., Nadal, F. & Eloy, C. 2011 Precessional instability of a fluid cylinder. J. Fluid Mech. 666, 104–145.Google Scholar
Landman, M. J. & Saffman, P. G. 1987 The three-dimensional instability of strained vortices in a viscous fluid. Phys. Fluids 30, 2339.Google Scholar
Lavorel, G. & Le Bars, M. 2010 Experimental study of the interaction between convective and elliptical instabilities. Phys. Fluids 22, 114101.Google Scholar
Le Bars, M., Lacaze, L., Le Dizès, S., Le Gal, P. & Rieutord, M. 2010 Tidal instability in stellar and planetary binary systems. Phys. Earth Planet. Inter. 178 (1–2), 48–55.Google Scholar
Le Bars, M., Le Dizès, S. & Le Gal, P. 2007 Coriolis effects on the elliptical instability in cylindrical and spherical rotating containers. J. Fluid Mech. 585, 323–342.Google Scholar
Le Bars, M., Wieczorek, M. A., Karatekin, Ö, Cébron, D. & Laneuville, M. 2011 An impact-driven dynamo for the early moon. Nature 479, 215–218.Google Scholar
Le Dizès, S. 2000 Three-dimensional instability of a multipolar vortex in a rotating flow. Phys. Fluids 12, 2762.Google Scholar
Le Dizès, S. & Eloy, C. 1999 Short-wavelength instability of a vortex in a multipolar strain field. Phys. Fluids 11, 500.Google Scholar
Leblanc, S. & Cambon, C. 1997 On the three-dimensional instabilities of plane flows subjected to Coriolis force. Phys. Fluids 9 (5), 1307–1316.CrossRefGoogle Scholar
Lebovitz, N. R. & Lifschitz, A. 1996 Short-wavelength instabilities of Riemann ellipsoids. Phil. Trans. R. Soc. Lond. A 354 (1709), 927–950.Google Scholar
Lifschitz, A. 1994 On the instability of certain motions of an ideal incompressible fluid. Adv. Appl. Math. 15 (4), 404–436.CrossRefGoogle Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids A: Fluid Dyn. 3, 2644.Google Scholar
Lifschitz, A. & Hameiri, E. 1993 Localized instabilities of vortex rings with swirl. Commun. Pure Appl. Maths 46 (10), 1379–1408.Google Scholar
Malkus, W. V. R. 1989 An experimental study of global instabilities due to the tidal (elliptical) distortion of a rotating elastic cylinder. Geophys. Astrophys. Fluid Dyn. 48 (1), 123–134.Google Scholar
Margot, J. L., Peale, S. J., Jurgens, R. F., Slade, M. A. & Holin, I. V. 2007 Large amplitude libration of Mercury reveals a molten core. Science 316 (5825), 710–714.Google Scholar
Mason, D. M. & Kerswell, R. R. 1999 Nonlinear evolution of the elliptical instability: an example of inertial wave breakdown. J. Fluid Mech. 396, 73–108.Google Scholar
Miyagoshi, T. & Hamano, Y. 2013 Magnetic field variation caused by rotational speed change in a magnetohydrodynamic dynamo. Phys. Rev. Lett. 111, 124501.Google Scholar
Moore, D. W. & Saffman, P. G. 1975 The instability of a straight vortex filament in a strain field. Proc. R. Soc. Lond. A 346 (1646), 413–425.Google Scholar
Noir, J., Calkins, M. A., Lasbleis, M., Cantwell, J. & Aurnou, J. M. 2010 Experimental study of libration-driven zonal flows in a straight cylinder. Phys. Earth Planet. Inter. 182 (1–2), 98–106.Google Scholar
Noir, J., Cébron, D., Le Bars, M., Sauret, A. & Aurnou, J. M. 2012 Experimental study of libration-driven zonal flows in non-axisymmetric containers. Phys. Earth Planet. Inter. 204/205, 1–10.Google Scholar
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173 (1–2), 141–152.Google Scholar
Poincaré, R. 1910 Sur la précession des corps déformables. Bull. Astron. I 27, 321–356.Google Scholar
Sauret, A., Cébron, D., Le Bars, M. & Le Dizès, S. et al. 2012 Fluid flows in a librating cylinder. Phys. Fluids 24, 026603.Google Scholar
Sauret, A., Cébron, D., Morize, C. & Le Bars, M. 2010 Experimental and numerical study of mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 662 (1), 260–268.CrossRefGoogle Scholar
Sauret, A. & Le Dizès, S. 2013 Libration-induced mean flow in a spherical shell. J. Fluid Mech. 718, 181–209.Google Scholar
Sipp, D. & Jacquin, L. 1998 Elliptic instability in two-dimensional flattened Taylor–Green vortices. Phys. Fluids 10, 839–849.Google Scholar
Tilgner, A. 1999 Driven inertial oscillations in spherical shells. Phys. Rev. E 59 (2), 1789–1794.CrossRefGoogle Scholar
Tsai, C. Y. & Widnall, S. E. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 73 (4), 721–733.Google Scholar
Vantieghem, S. 2011 Numerical simulations of quasi-static magnetohydrodynamics using an unstructured finite-volume solver: development and applications. PhD thesis, Université Libre de Bruxelles, Belgium.Google Scholar
Waleffe, F. 1990 On the three-dimensional instability of strained vortices. Phys. Fluids A: Fluid Dyn. 2, 76–80.Google Scholar
Wang, C. Y. 1970 Cylindrical tank of fluid oscillating about a state of steady rotation. J. Fluid Mech. 41 (3), 581–592.Google Scholar
Wieczorek, M. A. & Le Feuvre, M. 2009 Did a large impact reorient the Moon? Icarus 200 (2), 358–366.Google Scholar
Williams, J. G., Boggs, D. H., Yoder, C. F., Ratcliff, J. T. & Dickey, J. O. 2001 Lunar rotational dissipation in solid body and molten core. J. Geophys. Res. 106 (E11), 27 933–27 968.Google Scholar
Wu, C. C. & Roberts, P. H. 2013 On a dynamo driven topographically by longitudinal libration. Geophys. Astrophys. Fluid Dyn. 107 (1–2), 20–44.CrossRefGoogle Scholar
Zhang, K., Liao, X. & Earnshaw, P. 2004 On inertial waves and oscillations in a rapidly rotating spheroid. J. Fluid Mech. 504, 1–40.Google Scholar
Supplementary material: File

Cébron supplementary material

Supplementary Material

Download Cébron supplementary material(File)
File 6.3 KB