Article contents
A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition: transmission coefficient as an eigenvalue
Published online by Cambridge University Press: 30 March 2016
Abstract
This paper is concerned with the rather broad issue of the impact of abrupt changes (such as isolated roughness, gaps and local suctions) on boundary-layer transition. To fix the idea, we consider the influence of a two-dimensional localized hump (or indentation) on an oncoming Tollmien–Schlichting (T–S) wave. We show that when the length scale of the former is comparable with the characteristic wavelength of the latter, the key physical mechanism to affect transition is through scattering of T–S waves by the roughness-induced mean-flow distortion. An appropriate mathematical theory, consisting of the boundary-value problem governing the local scattering, is formulated based on triple deck formalism. The transmission coefficient, defined as the ratio of the amplitude of the T–S wave downstream of the roughness to that upstream, serves to characterize the impact on transition. The transmission coefficient appears as the eigenvalue of the discretized boundary-value problem. The latter is solved numerically, and the dependence of the eigenvalue on the height and width of the roughness and the frequency of the T–S wave is investigated. For a roughness element without causing separation, the transmission coefficient is found to be approximately 1.5 for typical frequencies, indicating a moderate but appreciable destabilizing effect. For a roughness causing incipient separation, the transmission coefficient can be as large as 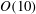 $O(10)$ , suggesting that immediate transition may take place at the roughness site. A roughness element with a fixed height produces the strongest impact when its width is comparable with the T–S wavelength, in which case the traditional linear stability theory is invalid. The latter however holds approximately when the roughness width is sufficiently large. By studying the two hump case, a criterion when two roughness elements can be regarded as being isolated is suggested. The transmission coefficient can be converted to an equivalent
$O(10)$ , suggesting that immediate transition may take place at the roughness site. A roughness element with a fixed height produces the strongest impact when its width is comparable with the T–S wavelength, in which case the traditional linear stability theory is invalid. The latter however holds approximately when the roughness width is sufficiently large. By studying the two hump case, a criterion when two roughness elements can be regarded as being isolated is suggested. The transmission coefficient can be converted to an equivalent  $N$ -factor increment, by making use of which the
$N$ -factor increment, by making use of which the 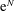 $\text{e}^{N}$ -method can be extended to predict transition in the presence of multiple roughness elements.
$\text{e}^{N}$ -method can be extended to predict transition in the presence of multiple roughness elements.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 50
- Cited by


