Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T23:05:44.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Mapping the properties of the vortex-induced vibrations of flexible cylinders in uniform oncoming flow

Published online by Cambridge University Press:  25 October 2019

Dixia Fan Open the ORCID record for Dixia Fan [Opens in a new window] ,
Zhicheng Wang Open the ORCID record for Zhicheng Wang [Opens in a new window] ,
Michael S. Triantafyllou Open the ORCID record for Michael S. Triantafyllou [Opens in a new window]  and
George Em Karniadakis
Dixia Fan
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute Technology, Cambridge, MA 02139, USA
Zhicheng Wang*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute Technology, Cambridge, MA 02139, USA
Michael S. Triantafyllou
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute Technology, Cambridge, MA 02139, USA
George Em Karniadakis
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
*
†Email address for correspondence: zhicheng@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Flexible structures placed within an oncoming flow exhibit far more complex vortex-induced dynamics than flexibly mounted rigid cylinders, because they involve the distributed interaction between the structural and wake dynamics along the entire span. Hence, mapping the well-understood properties of rigid cylinder vibrations to those of strings and beams has been elusive. We show here with a combination of experiments, conducted at Reynolds number, 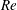$Re$ from 250 to 2300, and computational fluid dynamics that such a mapping is possible for flexible structures in uniform flow undergoing combined cross-flow and in-line oscillations, but only when additional concepts are introduced to model the extended coupling of the flow and the structure. The in-line response consists of largely standing waves that define cells, each cell spanning the distance between adjacent nodes, over which stable vortical patterns form, whose features (‘2S’ versus ‘P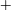$+$S’) depend strongly on the true reduced velocity, $V_{r}=U/f_{y}d$, where $U$ is the inflow velocity, 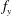$f_{y}$ is the cross-flow vibration frequency and 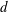$d$ is the cylinder diameter, and the phase angle between in-line and cross-flow response; while the cross-flow response may contain travelling waves, breaking the symmetry of the problem. The axial distribution of the highly variable effective added masses in the cross-flow and in-line directions, and the local phase angle between in-line and cross-flow motion determine the single frequency of cross-flow response, while the in-line response vibrates at twice the cross-flow frequency. The cross-flow and in-line lift coefficients in phase with velocity depend strongly on the true reduced velocity but also on the local phase angle between in-line and cross-flow motions. Modal shapes can be defined for in-line and cross-flow, based on the resemblance of the response to conventional modes, which can be in the ratio of either ‘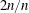$2n/n$’ or ‘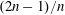$(2n-1)/n$’, where $n$ is the order of the cross-flow response mode. We use an underwater optical tracking system to reconstruct the sectional fluid forces in a flexible structure and show that, once the cross-flow and in-line motion features are known, employing strip theory and the hydrodynamic coefficients obtained from forced rigid cylinder experiments allows us to predict the distributed forces accurately.

JFM classification

Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 815 - 858
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aronsen, K. H.2007 An experimental investigation of in-line and combined in-line and cross-flow vortex induced vibrations. PhD thesis, Norwegian University of Science and Technology.Google Scholar
Bangash, Z. A. & Huera-Huarte, F. J. 2015 On the flow around the node to anti-node transition of a flexible cylinder undergoing vortex-induced vibrations. Phys. Fluids 27 (6), 065112.Google Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16 (1), 195–222.Google Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27 (5-6), 648–658.Google Scholar
Bishop, R. E. D. & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. A 277 (1368), 51–75.Google Scholar
Bourguet, R., Karniadakis, G. E. & Triantafyllou, M. S. 2013 Phasing mechanisms between the in-line and cross-flow vortex-induced vibrations of a long tensioned beam in shear flow. Comput. Struct. 122, 155–163.Google Scholar
Bourguet, R., Modarres-Sadeghi, Y., Karniadakis, G. E. & Triantafyllou, M. S. 2011 Wake-body resonance of long flexible structures is dominated by counterclockwise orbits. Phys. Rev. Lett. 107 (13), 134502.Google Scholar
Braaten, H. & Lie, H.2004 NDP riser high mode VIV tests. Tech. Rep. (512394.00), 01. Norwegian Marine Technology Research Institute.Google Scholar
Brika, D. & Laneville, A. 1993 Vortex-induced vibrations of a long flexible circular cylinder. J. Fluid Mech. 250, 481–508.Google Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2005 Controlled oscillations of a cylinder: forces and wake modes. J. Fluid Mech. 538, 31–69.Google Scholar
Chaplin, J. R., Bearman, P. W., Cheng, Y., Fontaine, E., Graham, J. M. R., Herfjord, K., Huera-Huarte, F. J., Isherwood, M., Lambrakos, K., Larsen, C. M. et al. 2005a Blind predictions of laboratory measurements of vortex-induced vibrations of a tension riser. J. Fluids Struct. 21 (1), 25–40.Google Scholar
Chaplin, J. R., Bearman, P. W., Huera-Huarte, F. J. & Pattenden, R. J. 2005b Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. J. Fluids Struct. 21 (1), 3–24.Google Scholar
Dahl, J. M.2008 Vortex-induced vibration of a circular cylinder with combined in-line and cross-flow motion. PhD thesis, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
Dahl, J. M., Hover, F. S. & Triantafyllou, M. S. 2006 Two-degree-of-freedom vortex-induced vibrations using a force assisted apparatus. J. Fluids Struct. 22 (6), 807–818.Google Scholar
Dahl, J. M., Hover, F. S. & Triantafyllou, M. S. 2008 High harmonic forces and predicted vibrations from forced in-line and cross-flow cylinder motions. In The 18th International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers.Google Scholar
Dahl, J. M., Hover, F. S., Triantafyllou, M. S., Dong, S. & Karniadakis, G. E. 2007 Resonant vibrations of bluff bodies cause multivortex shedding and high frequency forces. Phys. Rev. Lett. 99 (14), 144503.Google Scholar
Dahl, J. M., Hover, F. S., Triantafyllou, M. S. & Oakley, O. H. 2010 Dual resonance in vortex-induced vibrations at subcritical and supercritical Reynolds numbers. J. Fluid Mech. 643, 395–424.Google Scholar
Du, L., Jing, X. & Sun, X. 2014 Modes of vortex formation and transition to three-dimensionality in the wake of a freely vibrating cylinder. J. Fluids Struct. 49, 554–573.Google Scholar
Evangelinos, C. & Karniadakis, G. E. 1999 Dynamics and flow structures in the turbulent wake of rigid and flexible cylinders subject to vortex-induced vibrations. J. Fluid Mech. 400, 91–124.Google Scholar
Evangelinos, C., Lucor, D. & Karniadakis, G. E. 2000 DNS-derived force distribution on flexible cylinders subject to vortex-induced vibration. J. Fluids Struct. 14 (3), 429–440.Google Scholar
Facchinetti, M. L., De Langre, E. & Biolley, F. 2004 Coupling of structure and wake oscillators in vortex-induced vibrations. J. Fluids Struct. 19 (2), 123–140.Google Scholar
Fan, D., Du, H. & Triantafyllou, M. S. 2016 Optical tracking measurement on vortex-induced vibration of flexible riser with short-length buoyance module. In APS Fluid Dyn. Meeting Abstr. American Physical Society.Google Scholar
Fan, D. & Triantafyllou, M. S. 2017 Vortex-induced vibration of riser with low span to diameter ratio buoyancy modules. In The 27th International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers.Google Scholar
Gabbai, R. D. & Benaroya, H. 2005 An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 282 (3-5), 575–616.Google Scholar
Gilbert, S. & Sigurdson, L. 2010 The void structure in the wake of a self-oscillating flexible circular cylinder. Exp. Fluids 48 (3), 461–471.Google Scholar
Gopalkrishnan, R.1993 Vortex-induced forces on oscillating bluff cylinders. PhD thesis, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
GoPro Inc.2014 User manual: GoPro HERO 4 black.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
Govardhan, R. N. & Williamson, C. H. K. 2006 Defining the modified Griffin plot in vortex-induced vibration: revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 561, 147–180.Google Scholar
Guermond, J.-L., Pasquetti, R. & Popov, B. 2011a Entropy viscosity method for nonlinear conservation law. J. Comput. Phys. 230 (11), 4248–4267.Google Scholar
Guermond, J.-L., Pasquetti, R. & Popov, B. 2011b From suitable weak solutions to entropy viscosity. J. Sci. Comput. 49 (1), 35–50.Google Scholar
Han, Q., Ma, Y., Xu, W., Fan, D. & Wang, E. 2018 Hydrodynamic characteristics of an inclined slender flexible cylinder subjected to vortex-induced vibration. Inter. J. Mech. Sci. 148, 352–365.Google Scholar
Huera-Huarte, F. J. & Bearman, P. W. 2009a Wake structures and vortex-induced vibrations of a long flexible cylinder part 1: dynamic response. J. Fluids Struct. 25 (6), 969–990.Google Scholar
Huera-Huarte, F. J. & Bearman, P. W. 2009b Wake structures and vortex-induced vibrations of a long flexible cylinder part 2: drag coefficients and vortex modes. J. Fluids Struct. 25 (6), 991–1006.Google Scholar
Huera-Huarte, F. J., Bearman, P. W. & Chaplin, J. R. 2006 On the force distribution along the axis of a flexible circular cylinder undergoing multi-mode vortex-induced vibrations. J. Fluids Struct. 22 (6), 897–903.Google Scholar
Jauvtis, N. & Williamson, C. H. K. 2003 Vortex-induced vibration of a cylinder with two degrees of freedom. J. Fluids Struct. 17 (7), 1035–1042.Google Scholar
Jauvtis, N. & Williamson, C. H. K. 2004 The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 509, 23–62.Google Scholar
Karniadakis, G. E. & Sherwin, S. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics, 2nd edn. Oxford University Press.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7–8), 813–851.Google Scholar
Larsen, C. M., Vikestad, K., Yttervik, R., Passano, E. & Baarholm, G. S. 2001 Vivana Theory Manual. Marintek.Google Scholar
Modarres-Sadeghi, Y., Chasparis, F., Triantafyllou, M. S., Tognarelli, M. & Beynet, P. 2011 Chaotic response is a generic feature of vortex-induced vibrations of flexible risers. J. Sound Vib. 330 (11), 2565–2579.Google Scholar
Modarres-Sadeghi, Y., Mukundan, H., Dahl, J. M., Hover, F. S. & Triantafyllou, M. S. 2010 The effect of higher harmonic forces on fatigue life of marine risers. J. Sound Vib. 329 (1), 43–55.Google Scholar
Moeslund, T. B. & Granum, E. 2001 A survey of computer vision-based human motion capture. Comput. Vis. Image. Underst. 81 (3), 231–268.Google Scholar
Newman, D. J. & Karniadakis, G. E. 1996 Simulations of flow over a flexible cable: a comparison of forced and flow-induced vibration. J. Fluids Struct. 10 (5), 439–453.Google Scholar
Newman, D. J. & Karniadakis, G. E. 1997 A direct numerical simulation study of flow past a freely vibrating cable. J. Fluid Mech. 344, 95–136.Google Scholar
Raghavan, K. & Bernitsas, M. M. 2011 Experimental investigation of Reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports. Ocean Engng 38 (5-6), 719–731.Google Scholar
Roveri, F. E. & Vandiver, J. K. 2001 SlenderEx: using SHEAR7 for assessment of fatigue damage caused by current induced vibrations. In Proceedings of the 20th OMAE Conference, pp. 3–8. American Society of Mechanical Engineers.Google Scholar
Sarpkaya, T. 1978 Fluid forces on oscillating cylinders. NASA STI/Recon Tech. Rep. A 78, 275–290.Google Scholar
Sarpkaya, T. 1995 Hydrodynamic damping, flow-induced oscillations, and biharmonic response. J. Offshore Mech. Arctic Engng 117 (4), 232–238.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.Google Scholar
Staubli, T. 1983 Untersuchung der oszillierenden Kräfte am querangeströmten, schwingenden Kreiszylinder. ETH Zurich.Google Scholar
Tang, G., Lu, L., Teng, B., Park, H., Song, J. & Zhang, J. 2011 Identification of hydrodynamic coefficients from experiment of vortex-induced vibration of slender riser model. Sci. China Tech. Sci. 54 (7), 1894–1905.Google Scholar
Techet, A. H., Hover, F. S. & Triantafyllou, M. S. 1998 Vortical patterns behind a tapered cylinder oscillating transversely to a uniform flow. J. Fluid Mech. 363, 79–96.Google Scholar
Thompson, M., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12 (2), 190–196.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S., Tein, Y. S. & Ambrose, B. D. 1999 Pragmatic riser VIV analysis. In Offshore Technology Conference. Offshore Technology Conference.Google Scholar
Vandiver, J. K., Jaiswal, V. & Jhingran, V. 2009 Insights on vortex-induced, traveling waves on long risers. J. Fluids Struct. 25 (4), 641–653.Google Scholar
Vandiver, J. K., Swithenbank, S. B., Jaiswal, V. & Jhingran, V. 2006 Fatigue damage from high mode number vortex-induced vibration. In Proceedings of the 25th OMAE Conference, pp. 803–811. American Society of Mechanical Engineers.Google Scholar
Violette, R., De Langre, E. & Szydlowski, J. 2007 Computation of vortex-induced vibrations of long structures using a wake oscillator model: comparison with DNS and experiments. Comput. Struct. 85 (11–14), 1134–1141.Google Scholar
Wang, X., So, R. & Chan, K. 2003 A non-linear fluid force model for vortex-induced vibration of an elastic cylinder. J. Sound Vib. 260 (2), 287–305.Google Scholar
Wang, Z., Triantafyllou, M. S., Constantinides, Y. & Karniadakis, G. M. 2018 A spectral-element/Fourier smoothed profile method for large-eddy simulations of complex VIV problems. Comput. Fluids 172, 84–96.Google Scholar
Wang, Z., Triantafyllou, M. S., Constantinides, Y. & Karniadakis, G. M. 2019 An entropy-viscosity large eddy simulation study of turbulent flow in a flexible pipe. J. Fluid Mech. 859, 691–730.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2008 A brief review of recent results in vortex-induced vibrations. J. Wind Engng Ind. Aerodyn. 96 (6–7), 713–735.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.Google Scholar
Wu, J.2011 Hydrodynamic force identification from stochastic vortex induced vibration experiments with slender beams. PhD thesis, Norwegian University of Science and Technology.Google Scholar
Wu, J., Sheridan, J., Welsh, M. C. & Hourigan, K. 1996 Three-dimensional vortex structures in a cylinder wake. J. Fluid Mech. 312, 201–222.Google Scholar
Zheng, H., Dahl, J. M., Modarres-Sadeghi, Y. & Triantafyllou, M. S. 2014a Coupled inline-cross flow vortex-induced vibration hydrodynamic coefficients database. In ASME 2014 33th International Conference on Ocean, Offshore and Arctic Engeering, p. V002T08A087. American Society of Mechanical Engineers.Google Scholar
Zheng, H., Price, R. E., Modarres-Sadeghi, Y. & Triantafyllou, M. S. 2014b On fatigue damage of long flexible cylinders due to the higher harmonic force components and chaotic vortex-induced vibrations. Ocean Engng 88, 318–329.Google Scholar