Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T06:59:15.934Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurements of the budgets of the subgrid-scale stress and temperature flux in a convective atmospheric surface layer

Published online by Cambridge University Press:  24 July 2013

Khuong X. Nguyen ,
Thomas W. Horst ,
Steven P. Oncley  and
Chenning Tong
Khuong X. Nguyen
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
Thomas W. Horst
Affiliation:
National Center for Atmospheric Research, Boulder, CO 80307, USA
Steven P. Oncley
Affiliation:
National Center for Atmospheric Research, Boulder, CO 80307, USA
Chenning Tong*
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
*
†Email address for correspondence: ctong@ces.clemson.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of the subgrid-scale (SGS) stress and scalar flux in the convective atmospheric surface layer are studied through the budgets of the SGS turbulence kinetic energy (TKE), the SGS stress and the SGS temperature flux using field measurements from the Advection Horizontal Array Turbulence Study (AHATS). The array technique, which employs sensor arrays to perform filter operations to obtain the SGS velocity and temperature, is extended to include pressure sensors to measure the fluctuating pressure, enabling separation of the resolvable- and subgrid-scale pressure, and therefore for the first time allowing for measurement of the pressure covariance terms and the full SGS budgets. The non-dimensional forms of the SGS budget terms are obtained as functions of the stability parameter 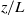$z/ L$ and the ratio of the wavelength of the spectral peak of the vertical velocity to the filter width, ${\Lambda }_{w} / {\Delta }_{f} $. The results show that the SGS TKE budget is a balance among the production, transport and dissipation. The SGS shear stress budget and the SGS temperature flux budgets are dominated by the production and pressure destruction, with the latter causing return to isotropy. The budgets of the SGS normal stress components are more complex. Most notably the pressure–strain-rate correlation includes two competing processes, return to isotropy and generation of anisotropy, the latter due to ground blockage of the large convective eddies. For neutral surface layers, return to isotropy dominates. For unstable surface layers return to isotropy dominates for small filter widths, whereas for large filter widths the ground blockage effect dominates, resulting in strong anisotropy. The results in the present study, particularly for the pressure–strain-rate correlation, have strong implications for modelling the SGS stress and flux using their transport equations in the convective atmospheric boundary layer.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 388 - 422
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bardina, J., Ferziger, J. H. & Reynolds, W. C. 1980 Improved subgrid-scale models for large-eddy simulation. AIAA Paper 80-1357.CrossRefGoogle Scholar
Borue, V. & Orszag, S. 1998 Local energy flux and subgrid-scale statistics in three-dimensional turbulence. J. Fluid Mech. 366, 1–31.CrossRefGoogle Scholar
Bou-Zeid, E., Higgins, C., Huwald, H., Meneveau, C. & Parlange, M. B. 2010 Field study of the dynamics and modelling of subgrid-scale turbulence in a stable atmospheric surface layer over a glacier. J. Fluid Mech. 665, 480–515.CrossRefGoogle Scholar
Bradley, E. F., Antonia, R. A. & Chambers, A. J. 1981 Turbulence Reynolds number and the turbulent kinetic energy balance in the atmospheric surface layer. Boundary-Layer Meteorol. 21, 183–197.CrossRefGoogle Scholar
Caughey, S. J. & Wyngaard, J. C. 1979 The turbulence kinetic energy budget in convective conditions. Q. J. R. Meteorol. Soc. 105, 231–239.CrossRefGoogle Scholar
Cerutti, S., Meneveau, C. & Knio, O. M. 2000 Spectral and hyper eddy viscosity in high-Reynolds-number turbulence. J. Fluid Mech. 421, 307–338.CrossRefGoogle Scholar
Chen, Q., Liu, S. & Tong, C. 2010 Investigation of the subgrid-scale fluxes and their production rates in a convective atmospheric surface layer using measurement data. J. Fluid Mech. 660, 282–315.CrossRefGoogle Scholar
Chen, Q. & Tong, C. 2006 Investigation of the subgrid-scale stress and its production rate in a convective atmospheric boundary layer using measurement data. J. Fluid Mech. 547, 65–104.CrossRefGoogle Scholar
Chen, Q., Zhang, H., Wang, D. & Tong, C. 2003 Subgrid-scale stress and its production rate: conditions for the resolvable-scale velocity probability density function. J. Turbul. 4, N27.CrossRefGoogle Scholar
Clark, R. A., Ferziger, J. H. & Reynolds, W. C. 1979 Evaluation of subgrid-scale models using an accurately simulated turbulent flow. J. Fluid Mech. 91, 1–16.CrossRefGoogle Scholar
Deardorff, J. W. 1970 A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 41, 453–480.CrossRefGoogle Scholar
Deardorff, J. W. 1972 Numerical investigation of neutral and unstable planetary boundary layers. J. Atmos. Sci. 29, 91–115.2.0.CO;2>CrossRefGoogle Scholar
Deardorff, J. W. 1973 The use of subgrid transport equations in a three-dimensional model of atmospheric turbulence. J. Fluids Engng 95, 429–438.CrossRefGoogle Scholar
Deardorff, J. W. 1980 Stratocumulus-capped mixed layers derived from a three-dimensional model. Boundary-Layer Meteorol. 18, 495–527.CrossRefGoogle Scholar
Domaradzki, J. A., Liu, W. & Brachet, M. E. 1993 An analysis of subgrid-scale interactions in numerically simulated isotropic turbulence. Phys. Fluids A 5, 1747–1759.CrossRefGoogle Scholar
Elliott, J. A. 1972 Microscale pressure fluctuations measured within the lower atmospheric boundary layer. J. Fluid Mech. 53, 351–383.CrossRefGoogle Scholar
Fu, S., Launder, B. E. & Tselepidakis, D. P. 1987 Accommodating the effects of high strain rates in modelling the pressure–strain correlation. Tech. Rep. Mechanical Engineering Department Report TFD/87/5, UMIST.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760–1765.CrossRefGoogle Scholar
Gibson, M. M. & Launder, B. E. 1978 Ground effects on pressure fluctuations in the atmospheric boundary layer. J. Fluid Mech. 86, 491–511.CrossRefGoogle Scholar
Hatlee, S. C. & Wyngaard, J. C. 2007 Improved subfilter-scale models from the HATS field data. J. Atmos. Sci. 64, 1694–1705.CrossRefGoogle Scholar
Higgins, C. W., Froidevaux, M., Simeonov, V., Vercauteren, N., Barry, C. & Parlange, M. B. 2012 The effect of scale on the applicability of Taylor’s frozen turbulence hypothesis in the atmospheric boundary layer. Boundary-Layer Meteorol. 143, 379–391.CrossRefGoogle Scholar
Higgins, C. W., Parlange, M. B. & Meneveau, C. 2007 The effect of filter dimension on the subgrid-scale stress, heat flux, and tensor alignments in the atmospheric surface layer. J. Atmos. Ocean. Tech. 24, 360–375.CrossRefGoogle Scholar
Högström, U. 1990 Analysis of turbulence structure in the surface layer with a modified similarity formulation for near neutral conditions. J. Atmos. Sci. 47, 1949–1972.2.0.CO;2>CrossRefGoogle Scholar
Horst, T. W., Kleissl, J., Lenschow, D. H., Meneveau, C., Moeng, C.-H., Parlange, M. B., Sullivan, P. P. & Weil, J. C. 2004 HATS: Field observations to obtain spatially-filtered turbulence fields from transverse arrays of sonic anemometers in the atmosperic surface flux layer. J. Atmos. Sci. 61, 1566–1581.2.0.CO;2>CrossRefGoogle Scholar
Kaimal, J. C. & Finnigan, J. J. 1994 Atmospheric Boundary Layer Flows. Oxford University Press.CrossRefGoogle Scholar
Kaimal, J. C., Wyngaard, J. C., Izumi, Y & Coté, O. R. 1972 Spectral characteristic of surface-layer turbulence. Q. J. R. Meteorol. Soc. 98, 563–589.Google Scholar
Khanna, S. & Brasseur, J. G. 1998 Three-dimensional buoyancy- and shear-induced local structure of the atmospheric boundary layer. J. Atmos. Sci. 55, 710–743.2.0.CO;2>CrossRefGoogle Scholar
Kleissl, J, Meneveau, C. & Parlange, M. 2003 On the magnitude and variability of subgrid-scale eddy-diffusion coefficients in the atmospheric surface layer. J. Atmos. Sci. 60, 2372–2388.2.0.CO;2>CrossRefGoogle Scholar
Kristensen, L., Mann, J., Oncley, S. P. & Wyngaard, J. C. 1997 How close is close enough when measuring scalar fluxes with displaced sensors? J. Atmos. Ocean. Tech. 14, 814–821.2.0.CO;2>CrossRefGoogle Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (3), 537–566.CrossRefGoogle Scholar
Lenschow, D. H., Mann, J. & Kristensen, L. 1993 How long is long enough when measuring fluxes and other turbulence statistics? Tech. Rep. NCAR/TN-389 + STR. National Center for Atmospheric Research.Google Scholar
Lenschow, D. H. & Raupach, M. R. 1991 The attenuation of fluctuations in scalar concentrations through sampling tubes. J. Geophys. Res. 96, 15259–15268.CrossRefGoogle Scholar
Leonard, A. 1974 Energy cascade in large-eddy simulations of turbulent fluid flows. Adv. in Geophys. 18, 237–248.CrossRefGoogle Scholar
Lilly, D. K. 1967 The representation of small-scale turbulence in numerical simulation experiments. In Proceedings IBM Scientific Computing Symposium on Environmental Science (ed. Goldstine, H. H.). pp. 195–210.Google Scholar
Ludwig, F. L., Chow, F. K. & Street, R. L. 2009 Effect of turbulence models and spatial resolution on resolved velocity structure and momentum fluxes in large-eddy simulations of neutral boundary layer flow. J. Appl. Meteorol. Climatol. 48, 1161–1180.CrossRefGoogle Scholar
Lumley, J. L. 1965 Interpretation of time spectra measured in high-intensity shear flows. Phys. Fluids 6, 1056–1062.CrossRefGoogle Scholar
Lumley, J. L. 1978 Computational modelling of turbulent flows. Adv. Appl. Mech. 18, 123–176.CrossRefGoogle Scholar
Lumley, J. L. 1983 Turbulence modelling. J. Appl. Mech. 50, 1097–1103.CrossRefGoogle Scholar
Mason, P. J. 1994 Large-eddy simulation: a critical review of the technique. Q. J. R. Meteorol. Soc. 120, 1–26.Google Scholar
Mason, P. J. & Brown, A. R. 1994 The sensitivity of large-eddy simulations of turbulent shear flow to subgrid models. Boundary-Layer Meteorol. 70, 133–150.CrossRefGoogle Scholar
Mason, P. J. & Thomson, D. J. 1992 Stochastic backscatter in large-eddy simulations of boundary layers. J. Fluid Mech. 242, 51–78.CrossRefGoogle Scholar
McBean, G. A. & Elliott, J. A. 1975 The vertical transports of kinetic energy by turbulence and pressure in the boundary layer. J. Atmos. Sci. 32, 753–766.2.0.CO;2>CrossRefGoogle Scholar
Meneveau, C., Lund, T. S. & Cabot, W. H. 1996 A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 319, 353–385.CrossRefGoogle Scholar
Métais, O. & Lesieur, M. 1992 Spectral large eddy simulation of isotropic and stably stratified turbulence. J. Fluid Mech. 239, 157–194.CrossRefGoogle Scholar
Miller, D. O., Tong, C. & Wyngaard, J. C. 1999 The effects of probe-induced flow distortion on velocity covariances: field observations. Boundary-Layer Meteorol. 91, 483–493.CrossRefGoogle Scholar
Nieuwstadt, F. T. M., Mason, P. J., Moeng, C.-H. & Schumann, U. 1991 Large-eddy simulation of the convective boundary layer: a comparison of four computer codes. In Turbulent Shear Flows 8 (ed. Durst, F., Friedrich, R., Launder, B. E., Schmidt, F. W., Schumann, U. & Whitelaw, J. H.), pp. 343–367. Springer.Google Scholar
Nieuwstadt, F. T. M. & de Valk, P. J. P. M. M. 1987 A large eddy simulation of buoyant and non-buoyant plume dispersion in the atmospheric boundary layer. Atmos. Environ. 21, 2573–2587.CrossRefGoogle Scholar
Nishiyama, R. T. & Bedard, A. J. 1991 A quad-disk static pressure probe for measurement in adverse atmospheres – with a comparative review of static pressure probe designs. Rev. Sci. Instrum. 62, 2193–2204.CrossRefGoogle Scholar
Patton, E. G., Horst, T. W., Sullivan, P. P., Lenschow, D. H., Oncley, S. P., Brown, W. O. J., Burns, S. P., Guenther, A. B., Held, A., Karl, T., Mayor, S. D., Rizzo, L. V., Spuler, S. M., Sun, J., Turnipseed, A. A., Allwine, E. J., Edburg, S. L., Lamb, B. K., Avissar, R., Calhoun, R. J., Kleissl, J., Massman, W. J., Paw-U, K. T. & Weil, J. C. 2011 The canopy horizontal array turbulence study. Bull. Amer. Meteorol. Soc. 92, 593–611.CrossRefGoogle Scholar
Peltier, L. J., Wyngaard, J. C., Khanna, S. & Brasseur, J. 1996 Spectra in the unstable surface layer. J. Atmos. Sci. 53, 49–61.2.0.CO;2>CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Porté-Agel, F., Parlange, M. B., Meneveau, C. & Eichinger, W. E. 2001 A priori field study of the subgrid-scale heat fluxes and dissipation in the atmospheric surface layer. J. Atmos. Sci. 58, 2673–2698.2.0.CO;2>CrossRefGoogle Scholar
Porté-Agel, F., Parlange, M. B., Meneveau, C., Eichinger, W. E. & Pahlow, M. 2000 Subgrid-scale dissipation in the atmospheric surface layer: effects of stability and filter dimension. J. Atmos. Sci. 1, 75–87.Google Scholar
Rajagopalan, A. G. & Tong, C. 2003 Experimental investigation of scalar–scalar-dissipation filtered joint density function and its transport equation. Phys. Fluids 15, 227–244.CrossRefGoogle Scholar
Ramachandran, S. & Wyngaard, J. C. 2011 Subfilter-scale modelling using transport equations: large-eddy simulation of the moderately convective atmospheric boundary layer. Boundary-Layer Meteorol. 139, 1–35.CrossRefGoogle Scholar
Rotta, J. C. 1951 Statistische theorie nichthomogener turbulenz. Z. Phys. 129, 547–572.CrossRefGoogle Scholar
Schumann, U. 1975 Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comput. Phys. 18, 376–404.CrossRefGoogle Scholar
Shih, T.-H. & Lumley, J. L. 1985 Modelling of pressure correlation terms in Reynolds stress and scalar flux equations. Tech. Rep. FDA 85-5. Cornell University.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: I. The basic equations. Mon. Weath. Rev. 91, 99–164.2.3.CO;2>CrossRefGoogle Scholar
Sullivan, P. P., Edson, J. B., Horst, T. W., Wyngaard, J. C. & Kelly, M. 2006 Subfilter scale fluxes in the marine surface layer: results from the ocean horizontal array turbulence study (OHATS). In 17th Symposium on Boundary Layers and Turbulence, San Diego, CA. American Meteorological Society.Google Scholar
Sullivan, P. P., Horst, T. W., Lenschow, D. H., Moeng, C.-H. & Weil, J. C. 2003 Structure of subfilter-scale fluxes in the atmospheric surface layer with application to large-eddy simulation modelling. J. Fluid Mech. 482, 101–139.CrossRefGoogle Scholar
Tong, C. 2001 Measurements of conserved scalar filtered density function in a turbulent jet. Phys. Fluids 13, 2923–2937.CrossRefGoogle Scholar
Tong, C., Wyngaard, J. C. & Brasseur, J. G. 1999 Experimental study of subgrid-scale stress in the atmospheric surface layer. J. Atmos. Sci. 56, 2277–2292.2.0.CO;2>CrossRefGoogle Scholar
Tong, C., Wyngaard, J. C., Khanna, S. & Brasseur, J. G. 1997 Resolvable- and subgrid-scale measurement in the atmospheric surface layer. In 12th Symposium on Boundary Layers and Turbulence, Vancouver, BC, Canada, pp. 221–222. American Meteorological Society.Google Scholar
Tong, C., Wyngaard, J. C., Khanna, S. & Brasseur, J. G. 1998 Resolvable- and subgrid-scale measurement in the atmospheric surface layer: technique and issues. J. Atmos. Sci. 55, 3114–3126.2.0.CO;2>CrossRefGoogle Scholar
Vreman, B., Geurts, B. & Kuerten, H. 1994 On the formulation of the dynamic mixed subgrid-scale model. Phys. Fluids 6, 4057–4059.CrossRefGoogle Scholar
Wang, D. & Tong, C. 2002 Conditionally filtered scalar dissipation, scalar diffusion, and velocity in a turbulent jet. Phys. Fluids 14, 2170–2185.CrossRefGoogle Scholar
Wang, D., Tong, C. & Pope, S. B. 2004 Experimental study of velocity filtered joint density function and its transport equation. Phys. Fluids 16, 3599–3613.CrossRefGoogle Scholar
Wilczak, J. M. & Bedard, A. J. 2004 A new turbulence microbarometer and its evaluation using the budget of horizontal heat flux. J. Atmos. Ocean. Tech. 21, 1170–1181.2.0.CO;2>CrossRefGoogle Scholar
Wilczak, J. M. & Businger, J. A. 1984 Large-scale eddies in the unstably stratified atmospheric surface layers. Part II: Turbulent pressure fluctuations and the budgets of heat flux, stress and turbulent kinetic energy. J. Atmos. Sci. 41, 3551–3567.2.0.CO;2>CrossRefGoogle Scholar
Wilczak, J. M., Oncley, S. P. & Stage, S. A. 2001 Sonic anemometer tilt correction algorithms. Boundary-Layer Meteorol. 99, 127–150.CrossRefGoogle Scholar
Wyngaard, J. C. 1971 Spatial resolution of a resistance wire temperature sensor. Phys. Fluids 14, 2052–2054.CrossRefGoogle Scholar
Wyngaard, J. C. 1981 The effects of probe-induced flow distortion on atmospheric turbulence measurements. J. Appl. Meteorol. 20, 784–794.2.0.CO;2>CrossRefGoogle Scholar
Wyngaard, J. C. 1992 Atmosperic turbulence. Annu. Rev. Fluid Mech. 24, 205–233.CrossRefGoogle Scholar
Wyngaard, J. C. 2004 Toward numerical modelling in the “terra incognita”. J. Atmos. Sci. 61, 1816–1826.2.0.CO;2>CrossRefGoogle Scholar
Wyngaard, J. C. & Coté, O. R. 1971 The budgets of turbulent kinetic energy and temperature variance in the atmospheric surface layer. J. Atmos. Sci. 28, 190–201.2.0.CO;2>CrossRefGoogle Scholar
Wyngaard, J. C., Coté, O. R. & Izumi, Y. 1971 Local free convection, similarity, and the budgets of shear stress and heat flux. J. Atmos. Sci. 28, 1171–1182.2.0.CO;2>CrossRefGoogle Scholar
Wyngaard, J. C., Siegel, A. & Wilczak, J. M. 1994 On the response of a turbulent-pressure probe and the measurement of pressure transport. Boundary-Layer Meteorol. 69, 379–396.CrossRefGoogle Scholar
Supplementary material: File

Nguyen et al. supplementary material

Supplementary figures 1-7

Download Nguyen et al. supplementary material(File)
File 6.1 MB