Article contents
Modelling and shock control for a V-shaped blunt leading edge
Published online by Cambridge University Press: 01 August 2023
Abstract
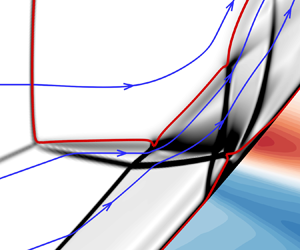
Hypersonic flow on a V-shaped blunt leading edge (VSBLE) at Mach 12 is numerically investigated. A series of self-induced shock–shock interactions and shock wave/boundary layer interactions (SWBLIs) cause extremely high heat flux peaks on the crotch of the VSBLE. Based on these shock structures, a simplified model that divides the flow field into inviscid and viscous areas is constructed. This model can quickly solve the shock interactions and predict the heating/pressure peaks with high accuracy. Furthermore, a shock control bump (SCB) is placed on the SWBLI region to split the strong incident shock into a weaker multi-wave system. The mechanism study of the SCB shows that the inviscid effect significantly reduces the heating/pressure peaks, and the viscous effect suppresses the SWBLI-induced separation. Finally, a VSBLE with SCBs is numerically investigated. The heat flux peak is reduced by 66 % compared to that without the SCBs. The robustness of the SCB under various working conditions is also evaluated. This paper provides an idea for the simplified solution of complex shock interactions and extends the application of the SCB as a thermal protection device in hypersonic flow for the first time.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 8
- Cited by


