Article contents
Modes and instabilities in magnetized spherical Couette flow
Published online by Cambridge University Press: 25 January 2013
Abstract
Several teams have reported peculiar frequency spectra for flows in a spherical shell. To address their origin, we perform numerical simulations of the spherical Couette flow in a dipolar magnetic field, in the configuration of the 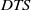 $DTS$ experiment. The frequency spectra computed from time-series of the induced magnetic field display similar bumpy spectra, where each bump corresponds to a given azimuthal mode number
$DTS$ experiment. The frequency spectra computed from time-series of the induced magnetic field display similar bumpy spectra, where each bump corresponds to a given azimuthal mode number 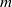 $m$ . The bumps appear at moderate Reynolds number (
$m$ . The bumps appear at moderate Reynolds number ( 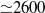 ${\simeq }2600$ ) if the time-series are long enough (
${\simeq }2600$ ) if the time-series are long enough ( 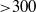 ${\gt }300$ rotations of the inner sphere). We present a new method that permits retrieval of the dominant frequencies for individual mode numbers
${\gt }300$ rotations of the inner sphere). We present a new method that permits retrieval of the dominant frequencies for individual mode numbers 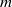 $m$ , and extraction of the modal structure of the full nonlinear flow. The maps of the energy of the fluctuations and the spatio-temporal evolution of the velocity field suggest that fluctuations originate in the outer boundary layer. The threshold of instability is found at
$m$ , and extraction of the modal structure of the full nonlinear flow. The maps of the energy of the fluctuations and the spatio-temporal evolution of the velocity field suggest that fluctuations originate in the outer boundary layer. The threshold of instability is found at 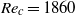 ${\mathit{Re}}_{c} = 1860$ . The fluctuations result from two coupled instabilities: high-latitude Bödewadt-type boundary layer instability, and secondary non-axisymmetric instability of a centripetal jet forming at the equator of the outer sphere. We explore the variation of the magnetic and kinetic energies with the input parameters, and show that a modified Elsasser number controls their evolution. We can thus compare with experimental determinations of these energies and find a good agreement. Because of the dipolar nature of the imposed magnetic field, the energy of magnetic fluctuations is much larger near the inner sphere, but their origin lies in velocity fluctuations that are initiated in the outer boundary layer.
${\mathit{Re}}_{c} = 1860$ . The fluctuations result from two coupled instabilities: high-latitude Bödewadt-type boundary layer instability, and secondary non-axisymmetric instability of a centripetal jet forming at the equator of the outer sphere. We explore the variation of the magnetic and kinetic energies with the input parameters, and show that a modified Elsasser number controls their evolution. We can thus compare with experimental determinations of these energies and find a good agreement. Because of the dipolar nature of the imposed magnetic field, the energy of magnetic fluctuations is much larger near the inner sphere, but their origin lies in velocity fluctuations that are initiated in the outer boundary layer.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
Footnotes
Current address: Facultad de Ciencias, Universidad Autónoma del Estado de Morelos, 62209, Cuernavaca Morelos, México.
References
Figueroa et al. supplementary movie
Map view of the time evolution of the azimuthal velocity uφ beneath the surface of the outer sphere (r = 0.95) in the reference numerical simulation (Pm = 10-3, Re = 2 611 and Λ = 3.4 _ 10-2). At the origin time, the fluid is at rest and the rotation rate of the inner sphere is set to f. Time t is measured in rotation periods of the inner sphere. There are 6 frames per turn and the movie lasts 100 turns. Note that the first instabilities appear at the equator and are axisymmetric. After about 24 turns, nonaxisymmetric instabilities show up.
- 32
- Cited by

