Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-31T02:10:49.431Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple resonances of a moving oscillating surface disturbance on a shear current

Published online by Cambridge University Press:  04 November 2016

Yan Li  and
Simen Å. Ellingsen Open the ORCID record for Simen Å. Ellingsen [Opens in a new window]
Yan Li*
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
Simen Å. Ellingsen
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
*
†Email address for correspondence: yan.li@ntnu.no
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider waves radiated by a disturbance of oscillating strength moving at constant velocity along the free surface of a shear flow, which, when undisturbed, has uniform horizontal vorticity of magnitude 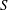$S$. When no current is present the problem is a classical one and much studied, and in deep water a resonance is known to occur when $\unicode[STIX]{x1D70F}=|\boldsymbol{V}|\unicode[STIX]{x1D714}_{0}/g$ equals the critical value 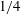$1/4$ (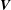$\boldsymbol{V}$: velocity of disturbance, 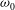$\unicode[STIX]{x1D714}_{0}$: oscillation frequency, 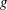$g$: gravitational acceleration). We show that the presence of a subsurface shear current can change this picture radically. Not only does the resonant value of $\unicode[STIX]{x1D70F}$ depend strongly on the angle between 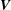$\boldsymbol{V}$ and the current’s direction and the ‘shear-Froude number’ 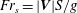$\mathit{Fr}_{s}=|\boldsymbol{V}|S/g$; when 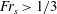$\mathit{Fr}_{s}>1/3$, multiple resonant values – as many as four – can occur for some directions of motion. At sufficiently large values of 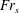$\mathit{Fr}_{s}$, the smallest resonance frequency tends to zero, representing the phenomenon of critical velocity for ship waves. We provide a detailed analysis of the dispersion relation for the moving oscillating disturbance, in both finite and infinite water depth, including for the latter case an overview of the different far-field waves which exist in different sectors of wave-vector space under different conditions. Owing to the large number of parameters, a detailed discussion of the structure of resonances is provided for infinite depth only, where analytical results are available.

JFM classification

Waves/Free-surface Flows: Shear waves Waves/Free-surface Flows: Surface gravity waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , pp. 668 - 689
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akylas, T. R. 1984 On the excitation of long nonlinear water waves by a moving pressure distribution. J. Fluid Mech. 141, 455–466.CrossRefGoogle Scholar
Becker, E. 1956 Die pulsierende Quelle unter der freien Oberfläche eines Stromes endlicher Tiefe. Ing.-Arch. 24, 69–76.CrossRefGoogle Scholar
Becker, E. 1958 Das Wellenbild einer unter der Oberfläche eines Stromes schwerer Flüssigkeit pulsierenden Quelle. Z. Angew. Math. Mech. J. Appl. Math. Mech. 38, 391–399.CrossRefGoogle Scholar
Brard, R. 1948 Introduction à l’étude théorique du tangage en marche. Bull. Assoc. Tech. Maritim. Aeronaut. 47, 455–479.Google Scholar
Charland, J., Toubol, J. & Rey, V. 2012 Propagation de la houle à contre-courant: etude de l’impact de cisaillements horizontaux et verticaux du courant moyen sur la focalisation géométrique de la houle. In Proc. Les 13èmes Journées de l’Hydrodynamique, Chatou, France, pp. 21–23. Ecole Centrale de Nantes.Google Scholar
Dagan, G. & Miloh, T. 1980 Flow past oscillating bodies at resonant frequency. In Proceedings of 13th Symposium Naval Hydrodynamics (ed. Inui, T.), pp. 355–373. The Shipbuilding Research Association of Japan.Google Scholar
Dagan, G. & Miloh, T. 1982 Free-surface flow past oscillating singularities at resonant frequency. J. Fluid Mech. 120, 139–154.Google Scholar
Debnath, L. 1969 On three dimensional transient wave motions on a running stream. Meccanica 4, 122–128.CrossRefGoogle Scholar
Debnath, L. & Rosenblat, S. 1969 The ultimate approach to the steady state in the generation of waves on a running stream. Q. J. Mech. Appl. Maths 22, 221–233.CrossRefGoogle Scholar
Doctors, L. J. 1978 Hydrodynamic power radiated by a heaving and pitching air-cushion vehicle. J. Ship Res. 22, 67–79.Google Scholar
Dong, Z. & Kirby, J. T. 2012 Theoretical and numerical study of wave–current interaction in strongly-sheared flows. In Proceedings of 33rd Conference on Coastal Engineering (ed. Lynett, P. & McKee Smith, J.). The Coastal Engineering Research Council.Google Scholar
Eggers, K. 1957 Über das Wellenbild einer pulsierenden Störung in Translation. Schiff Hafen 11, 90–98.Google Scholar
Ellingsen, S. Å. 2014a Initial surface disturbance on a shear current: the Cauchy–Poisson problem with a twist. Phys. Fluids 26, 082104.Google Scholar
Ellingsen, S. Å. 2014b Ship waves in the presence of uniform vorticity. J. Fluid Mech. 742, R2.Google Scholar
Ellingsen, S. Å. & Tyvand, P. A. 2016a Oscillating line source in a shear flow with a free surface: critical layer contributions. J. Fluid Mech. 798, 201–231.CrossRefGoogle Scholar
Ellingsen, S. Å. & Tyvand, P. A. 2016b Waves from an oscillating point source with a free surface in the presence of a shear current. J. Fluid Mech. 798, 232–255.CrossRefGoogle Scholar
Ertekin, R. C., Webster, W. C. & Wehausen, J. V. 1986 Waves caused by a moving disturbance in a shallow channel of finite width. J. Fluid Mech. 169, 275–292.Google Scholar
Grue, J. 1986 Time-periodic wave loading on a submerged circular cylinder in a current. J. Ship Res. 30, 153–158.Google Scholar
Grue, J. & Palm, E. 1985 Wave radiation and wave diffraction from a submerged body in a uniform current. J. Fluid Mech. 151, 257–278.CrossRefGoogle Scholar
Haskind, M. D. 1946 The hydrodynamic theory of ship oscillations in rolling and pitching. Prikl. Mat. Mekh. 10, 33–66.Google Scholar
Haskind, M. D. 1954 On wave motion of a heavy fluid. Prikl. Mat. Mekh. 18, 15–26.Google Scholar
Havelock, T. H. 1908 The propagation of groups of waves in dispersive media, with application to waves on water produced by a travelling disturbance. Proc. R. Soc. Lond. A 81, 398–430.Google Scholar
Havelock, T. H. 1958 The effect of speed of advance upon the damping of heave and pitch. Trans. Inst. Naval Arch. I 100, 131–135.Google Scholar
Kaplan, P. 1957 The waves generated by the forward motion of oscillatory pressure distributions. In Proceedings of 5th Midwest. Conference on Fluid Mechanics, Ann Arbor, Michigan (ed. Kluether, A. M.), pp. 316–329. The University of Michigan Press.Google Scholar
Katsis, C. & Akylas, T. R. 1987 On the excitation of long nonlinear water waves by a moving pressure distribution. Part 2. Three-dimensional effects. J. Fluid Mech. 177, 49–65.CrossRefGoogle Scholar
Kilcher, L. F. & Nash, J. D. 2010 Structure and dynamics of the Columbia River tidal plume front. J. Geophys. Res. Oceans 115, C05590.CrossRefGoogle Scholar
Kring, D. C. 1998 Ship seakeeping through the 𝜏 = 1/4 critical frequency. J. Ship Res. 42, 113–119.Google Scholar
Lee, S.-J., Yates, G. T. & Wu, T. Y. 1989 Experiments and analyses of upstream-advancing solitary waves generated by moving disturbances. J. Fluid Mech. 199, 569–593.Google Scholar
Li, Y. & Ellingsen, S. Å. 2015 Initial value problems for water waves in the presence of a shear current. In Proceedings of the 25th International Offshore and Polar Engineering Conference (ISOPE) (ed. Chung, J. S., Vorpahl, F., Hong, S. Y., Kokkinis, T. & Wang, A. W.), pp. 543–549. The International Society of Offshore and Polar Engineers.Google Scholar
Li, Y. & Ellingsen, S. Å. 2016 Ship waves on uniform shear current at finite depth: wave resistance and critical velocity. J. Fluid Mech. 791, 539–567.CrossRefGoogle Scholar
Lighthill, M. J. 1970 On waves generated in dispersive systems by travelling forcing effects, with applications to the dynamics of rotating fluids. In Hyperbolic Equations and Waves, pp. 124–152. Springer.CrossRefGoogle Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Liu, Y. & Yue, D. K.-P. 1993 On the solution near the critical frequency for an oscillating and translating body in or near a free surface. J. Fluid Mech. 254, 251–266.CrossRefGoogle Scholar
Lunde, J. K.1951 On the linearized theory of wave resistance for a pressure distribution moving at constant speed of advance on the surface of deep or shallow water. Tech. Rep. 8, Skipsmodelltanken, Norges Tekniske Høgskole, Trondheim, Norway.Google Scholar
Maruo, H. & Matsunaga, K. 1983 The slender body approximation in radiation and diffraction problems of a ship with forward speed. In Proceedings of the 12th Sci. Methodol. Semin. Ship Hydrodynamics (SMSSH).Google Scholar
Mei, C. C., Stiassnie, M. & Yue, D. K.-P. 2005 Theory and Applications of Ocean Surface Waves. Part 1: Linear Aspects, Advanced Series on Ocean Engineering, vol. 23. World Scientific.Google Scholar
Newman, J. N. 1959 The damping and wave resistance of a pitching and heaving ship. J. Ship Res. 3, 1–19.Google Scholar
Peregrine, D. H. 1976 Interaction of water waves and currents. Adv. Appl. Mech. 16, 9–117.CrossRefGoogle Scholar
Pramanik, A. K. 1980 Capillary-gravity waves produced by a moving pressure distribution. Z. Angew. Math. Phys. 31, 174–180.CrossRefGoogle Scholar
Tayler, A. & van den Driessche, P. 1974 Small amplitude surface waves due to a moving source. Q. J. Mech. Appl. Maths 27, 317–345.Google Scholar
Tyvand, P. A. & Lepperød, M. E. 2014 Oscillatory line source for water waves in shear flow. Wave Motion 51, 505–516.CrossRefGoogle Scholar
Tyvand, P. A. & Lepperød, M. E. 2015 Doppler effects of an oscillating line source in shear flow with a free surface. Wave Motion 52, 103–119.Google Scholar
Wehausen, J. W. & Laitone, E. V. 1960 Surface waves. In Fluid Dynamics III (ed. Flügge, S.), Encyclopedia of Physics, vol. IX, pp. 446–778. Springer.Google Scholar
Wu, T.1957 Water waves generated by the translatory and oscillatory surface disturbance. Tech. Rep. 85-3, California Institute of Technology.Google Scholar