Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T01:58:19.311Z Has data issue: false hasContentIssue false
  • English
  • Français

A new scaling for the flow instability past symmetric bluff bodies

Published online by Cambridge University Press:  15 February 2022

A. Chiarini Open the ORCID record for A. Chiarini [Opens in a new window] ,
M. Quadrio Open the ORCID record for M. Quadrio [Opens in a new window]  and
F. Auteri Open the ORCID record for F. Auteri [Opens in a new window]
A. Chiarini
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
M. Quadrio
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
F. Auteri*
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
*
†Email address for correspondence: franco.auteri@polimi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

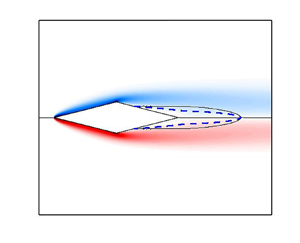
A scaling law to predict the onset of the primary Hopf instability in the steady flow past two-dimensional symmetric bluff bodies is proposed. It uses a measure of the spatial extent of the separation bubble as the length scale and the largest reverse-flow speed within it as the velocity scale. The ensuing Reynolds number, evaluated at the onset of the primary Hopf bifurcation, collapses quite nicely for bodies of different shape and aspect ratio even when a small angle of attack perturbs the symmetry; its relative variation is one order of magnitude smaller than that of the usual Reynolds number defined with the free-stream velocity and the cross-stream body size. With the new scaling, it can be roughly assessed whether the steady flow past a two-dimensional bluff body is absolutely and globally unstable to two-dimensional perturbations without a computationally expensive stability analysis: only the inspection of the base flow is required. More importantly, the scaling provides an insight into the flow mechanism that produces the instability.

JFM classification

Wakes/Jets: Separated flows Wakes/Jets: Vortex streets Instability: Absolute/convective instability
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 936 , 10 April 2022 , R2
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Chiarini, A., Quadrio, M. & Auteri, F. 2021 Linear stability of the steady flow past rectangular cylinders. J. Fluid Mech. 929, A36.CrossRefGoogle Scholar
Chiarini, A., Quadrio, M. & Auteri, F. 2022 On the frequency selection mechanism of the low-Re flow around rectangular cylinders. J. Fluid Mech. 933, A44.CrossRefGoogle Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flowa: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37 (1), 357–392.CrossRefGoogle Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Hammond, D.A. & Redekopp, L.G. 1997 Global dynamics of symmetric and asymmetric wakes. J. Fluid Mech. 331, 231–260.CrossRefGoogle Scholar
Hecht, F. 2012 New development in FreeFem++. J. Numer. Maths 20 (3–4), 251–266.Google Scholar
Hourigan, K., Thompson, M.C. & Tan, B.T. 2001 Self-sustained oscillations in flows around long blunt plates. J. Fluids Struct. 15 (3), 387–398.CrossRefGoogle Scholar
Jackson, C.P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.CrossRefGoogle Scholar
Lehoucq, R.B., Sorensen, D.C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Mat Ali, M.S., Doolan, C.J. & Wheatley, V. 2011 Low Reynolds number flow over a square cylinder with a splitter plate. Phys. Fluids 23 (3), 033602.CrossRefGoogle Scholar
Monkewitz, P.A., Huerre, P. & Chomaz, J.-M. 1993 Global linear stability analysis of weakly non-parallel shear flows. J. Fluid Mech. 251, 1–20.CrossRefGoogle Scholar
Ng, Z.Y., Vo, T., Hussam, W.K. & Sheard, G.J. 2016 Two-dimensional wake dynamics behind cylinders with triangular cross-section under incidence angle variation. J. Fluids Struct. 63, 302–324.CrossRefGoogle Scholar
Noack, B.R. & Eckelmann, H. 1994 A global stability analysis of the steady and periodic cylinder wake. J. Fluid Mech. 270, 297–330.CrossRefGoogle Scholar
Okajima, A. 1982 Strouhal numbers of rectangular cylinders. J. Fluid Mech. 123, 379–398.CrossRefGoogle Scholar
Park, D. & Yang, K.-S. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Prhashanna, A., Sahu, A.K. & Chhabra, R.P. 2011 Flow of power-law fluids past an equilateral triangular cylinder: momentum and heat transfer characteristics. Intl J. Therm. Sci. 50 (10), 2027–2041.CrossRefGoogle Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Saad, Y. 2011 Numerical Methods for Large Eigenvalue Problems. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Thompson, M.C., Radi, A., Rao, A., Sheridan, J. & Hourigan, K. 2014 Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate. J. Fluid Mech. 751, 570–600.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Yoon, D.-H., Yang, K.-S. & Choi, C.-B. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22 (4), 043603.CrossRefGoogle Scholar