Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T07:59:07.378Z Has data issue: false hasContentIssue false
  • English
  • Français

New scaling laws for turbulent Poiseuille flow with wall transpiration

Published online by Cambridge University Press:  28 March 2014

V. Avsarkisov ,
M. Oberlack  and
S. Hoyas
V. Avsarkisov*
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, Otto-Berndt-Strasse 2, 64287 Darmstadt, Germany
M. Oberlack*
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, Otto-Berndt-Strasse 2, 64287 Darmstadt, Germany Centre of Smart Interfaces, TU Darmstadt, Alarich-Weiss-Strasse 10, 64287 Darmstadt, Germany GS Computational Engineering, TU Darmstadt, Dolivostrasse 15, 64293 Darmstadt, Germany
S. Hoyas
Affiliation:
CMT Motores Térmicos, Universitat Politècnica de València, València, Spain
*
†Email addresses for correspondence: v.avsarkisov@astro-ge.org, oberlack@fdy.tu-darmstadt.de
†Email addresses for correspondence: v.avsarkisov@astro-ge.org, oberlack@fdy.tu-darmstadt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

A fully developed, turbulent Poiseuille flow with wall transpiration, i.e. uniform blowing and suction on the lower and upper walls correspondingly, is investigated by both direct numerical simulation (DNS) of the three-dimensional, incompressible Navier–Stokes equations and Lie symmetry analysis. The latter is used to find symmetry transformations and in turn to derive invariant solutions of the set of two- and multi-point correlation equations. We show that the transpiration velocity is a symmetry breaking which implies a logarithmic scaling law in the core of the channel. DNS validates this result of Lie symmetry analysis and hence aids establishing a new logarithmic law of deficit type. The region of validity of the new logarithmic law is very different from the usual near-wall log law and the slope constant in the core region differs from the von Kármán constant and is equal to 0.3. Further, extended forms of the linear viscous sublayer law and the near-wall log law are also derived, which, as a particular case, include these laws for the classical non-transpiring case. The viscous sublayer at the suction side has an asymptotic suction profile. The thickness of the sublayer increase at high Reynolds and transpiration numbers. For the near-wall log law we see an indication that it appears at the moderate transpiration rates (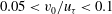$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}0.05<v_0/u_{\tau }<0.1$) and only at the blowing wall. Finally, from the DNS data we establish a relation between the friction velocity 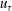$u_{\tau }$ and the transpiration 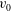$v_0$ which turns out to be linear at moderate transpiration rates.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 746 , 10 May 2014 , pp. 99 - 122
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

The original version of this article was published with the incorrect affiliation for S. Hoyas. A notice detailing this has been published online and in print, and the error rectified in the online PDF and HTML copies.

References

Antonia, R. S., Krishnamoorthy, L. V., Fulachier, L., Anselmet, F. & Benabid, T.1986 Influence of wall suction on coherent structures in a turbulent boundary layer. In 9th Australasian Fluid Mechanics Conference, Auckland, Australia, pp. 346–349.Google Scholar
Avsarkisov, V. S., Oberlack, M. & Khujadze, G. 2011 Turbulent Poiseuille flow with wall-transpiration: analytical study and direct numerical simulation. J. Phys.: Conf. Ser. 318, 022004.Google Scholar
Black, T. J. & Sarnecki, A. J.1958 The turbulent boundary layer with suction or injection. Tech. Rep. 20, Cambrige University, Engineering Department.Google Scholar
Bluman, G. W., Cheviakov, A. F. & Anco, S. C. 2010 Application of Symmetry Methods to Partial Differential Equations. Springer.CrossRefGoogle Scholar
Chung, Y. M. & Sung, H. J. 2001 Initial relaxation of spatially evolving turbulent channel flow with blowing and suction. AIAA J. 39 (11), 2091–2099.CrossRefGoogle Scholar
Chung, Y. M., Sung, H. J. & Krogstad, P.-A. 2002 Modulation of near-wall turbulence structure with wall blowing and suction. AIAA J. 40 (8), 1529–1535.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), 41–44.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Drazin, P. G. & Riley, N. 2006 The Navier–Stokes Equations: A Classification of Flows and Exact Solutions. Cambridge University Press.CrossRefGoogle Scholar
El Telbany, M. M. M. & Reynolds, A. J. 1981 Turbulence in plane channel flows. J. Fluid Mech. 111, 283–318.CrossRefGoogle Scholar
Fife, P., Klewicki, J. C. & Wei, T. 2009 Time averaging in turbulence settings may reveal an infinite hierarchy of length scales. J. Discrete Continuous Dyn. Syst. 24 (3), 781–807.CrossRefGoogle Scholar
Griffith, A. A. & Meredith, F. W.1936 Possible improvement in aircraft performance due to use of boundary layer suction. Tech. Rep. 2315, Aero. Res. Counc., London.Google Scholar
Hanjalić, K. & Launder, B. E. 1972a Fully developed asymmetric flow in a plane channel. J. Fluid Mech. 51 (2), 301–335.CrossRefGoogle Scholar
Hanjalić, K. & Launder, B. E. 1972b Reynolds-stress model of turbulence and its application to thin shear flows. J. Fluid Mech. 52 (4), 609–638.CrossRefGoogle Scholar
Hinze, J. O. 1959 Turbulence, An Introduction to its Mechanism and Theory. McGraw-Hill.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $\textit {Re}_{\tau }=2003$ . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.CrossRefGoogle Scholar
Jiménez, J., Uhlmann, M., Pinelli, M. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.CrossRefGoogle Scholar
Johnstone, R., Coleman, G. N. & Spalart, P. R. 2010 The resilience of the logarithmic law to pressure gradients: evidence from direct numerical simulation. J. Fluid Mech. 643, 163–175.CrossRefGoogle Scholar
Kametani, Y. & Fukagata, K. 2011 Direct numerical simulation of spatially developing turbulent boundary layer with uniform blowing or suction. J. Fluid Mech. 681, 154–172.CrossRefGoogle Scholar
Keller, L. & Friedmann, A.1924 Differentialgleichungen für die turbulente Bewegung einer kompressiblen Flüssigkeit. In Proc. First. Int. Congr. Appl. Mech., pp. 395–405.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Klewicki, J. C. 2013 Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–612.CrossRefGoogle Scholar
Kraichnan, R. H. 1965 Lagrangian-history closure approximaiton for turbulence. Phys. Fluids 8 (4), 575–598.CrossRefGoogle Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (3), 537–566.CrossRefGoogle Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.CrossRefGoogle Scholar
Lindgren, B., Österlund, J. M. & Johansson, A. V. 2004 Evaluation of scaling laws derived from lie group symmetry methods in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 502, 127–152.CrossRefGoogle Scholar
McComb, W. D. 1990 The Physics of Fluid Turbulence. Oxford University Press.CrossRefGoogle Scholar
Mickley, H. S. & Davis, R. S. 1957 Momentum Transfer for Flow Over a Flat Plate with Blowing. In Tech. Rep., vol. 4017. MIT.Google Scholar
Millikan, C. B.1939 A critical discussion of turbulent flows in channels and circular tubes. In Proc. Vth Int. Congr. Appl. Mech., pp. 386–392.Google Scholar
Nakabayashi, K., Kitoh, O. & Katoh, Y. 2004 Similarity laws of velocity profiles and turbulence characteristics of Couette–Poiseuille turbulent flows. J. Fluid Mech. 507, 43–69.CrossRefGoogle Scholar
Nikitin, N. V. & Pavel’ev, A. A. 1998 Turbulent flow in a channel with permeable walls. DNS and results of three-parameter-model. J. Fluid Mech. 33 (6), 826–832.Google Scholar
Oberlack, M.2000 Symmetrie, Invarianz und Selbstähnlichkeit in der Turbulenz. Habilitation thesis.Google Scholar
Oberlack, M. 2001 A unified approach for symmetries in plane parallel turbulent shear flows. J. Fluid Mech. 427, 299–328.CrossRefGoogle Scholar
Oberlack, M. & Rosteck, A. 2010 New statistical symmetries of the multi-point equations and its importance for turbulent scaling laws. Discrete Continuous Dyn. Syst. S 3 (3), 451–471.CrossRefGoogle Scholar
Rosteck, A. & Oberlack, M. 2011 Lie algebra of the symmetries of the multi-point equations in statistical turbulence theory. J. Nonlinear Math. Phys. 18, 251–264.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2011 Turbulent asymptotic suction boundary layers studied by simulation. J. Phys.: Conf. Ser. 318, 1–10.Google Scholar
Stevenson, T. N. 1963a A Law of the Wall for Turbulent Boundary Layers with Suction or Injection. In Tech. Rep., vol. 166. The College of Aeronautics Cranfield.Google Scholar
Stevenson, T. N. 1963b 1963b A modified velocity defect law for turbulent boundary layers with injection. Tech. Rep. 170 The College of Aeronautics Cranfield.Google Scholar
Sumitani, Y. & Kasagi, N. 1995 Direct numerical simulation of turbulent transport with uniform wall injection and suction. AIAA J. 33 (7), 1220–1228.CrossRefGoogle Scholar
Tennekes, H. 1965 Similarity laws for turbulent boundary layers with suction or injection. J. Fluid Mech. 21 (4), 689–703.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. The MIT Press.CrossRefGoogle Scholar
Vigdorovich, I. & Oberlack, M. 2008 Analytical study of turbulent Poiseuille flow with wall-transpiration. Phys. Fluids 20, 055102.CrossRefGoogle Scholar
von Kármán, Th. 1930 Mechanische Ähnlichkeit und Turbulentz, Nachr. Ges. Wiss. Göettingen, Math-Phys. Kl., vol. 68.Google Scholar
von Kármán, Th. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164, 192–215.CrossRefGoogle Scholar
Wei, T., Fife, P. & Klewicki, J. 2007 On scaling the mean momentum balance and its solutions in turbulent Couette–Poiseuille flow. J. Fluid Mech. 573, 371–398.CrossRefGoogle Scholar
Wosnik, M., Castillo, L. & George, W. K. 2000 A theory for turbulent pipe and channel flows. J. Fluid Mech. 421, 115–145.CrossRefGoogle Scholar
Zhapbasbayev, U. & Isakhanova, G. 1998 Developed turbulent flow in a plane channel with simultaneous injection through one porous wall and suction through the other. J. Appl. Mech. Tech. Phys. 39, 53–59.CrossRefGoogle Scholar