Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-09T19:44:40.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear electrophoretic velocity of a spherical colloidal particle

Published online by Cambridge University Press:  31 July 2023

Richard Cobos Open the ORCID record for Richard Cobos [Opens in a new window]  and
Aditya S. Khair Open the ORCID record for Aditya S. Khair [Opens in a new window]
Richard Cobos
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Aditya S. Khair*
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
*
†Email address for correspondence: akhair@andrew.cmu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

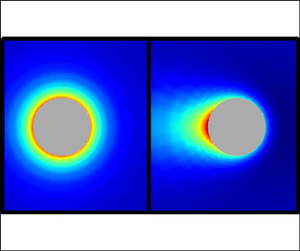
Electrophoresis is the motion of a charged colloidal particle in an electrolyte under an applied electric field. The electrophoretic velocity of a spherical particle depends on the dimensionless electric field strength $\beta =a^*e^*E_\infty ^*/k_B^*T^*$, defined as the ratio of the product of the applied electric field magnitude $E_\infty ^*$ and particle radius $a^*$, to the thermal voltage $k_B^*T^*/e^*$, where $k_B^*$ is Boltzmann's constant, $T^*$ is the absolute temperature, and $e^*$ is the charge on a proton. In this paper, we develop a spectral element algorithm to compute the electrophoretic velocity of a spherical, rigid, dielectric particle, of fixed dimensionless surface charge density $\sigma$ over a wide range of $\beta$. Here, $\sigma =(e^*a^*/\epsilon ^*k_B^*T^*)\sigma ^*$, where $\sigma ^*$ is the dimensional surface charge density, and $\epsilon ^*$ is the permittivity of the electrolyte. For moderately charged particles ($\sigma ={O}(1)$), the electrophoretic velocity is linear in $\beta$ when $\beta \ll 1$, and its dependence on the ratio of the Debye length ($1/\kappa ^*$) to particle radius (denoted by $\delta =1/(\kappa ^*a^*)$) agrees with Henry's formula. As $\beta$ increases, the nonlinear contribution to the electrophoretic velocity becomes prominent, and the onset of this behaviour is $\delta$-dependent. For $\beta \gg 1$, the electrophoretic velocity again becomes linear in field strength, approaching the Hückel limit of electrophoresis in a dielectric medium, for all $\delta$. For highly charged particles ($\sigma \gg 1$) in the thin-Debye-layer limit ($\delta \ll 1$), our computations are in good agreement with recent experimental and asymptotic results.

JFM classification

Complex Fluids: Colloids MHD and Electrohydrodynamics: Electrokinetic flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 968 , 10 August 2023 , A14
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J.L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 21 (1), 61–99.CrossRefGoogle Scholar
Antunez-Vela, S., Perez-Gonzalez, V.H., De Peña, A.C., Lentz, C.J. & Lapizco-Encinas, B.H. 2020 Simultaneous determination of linear and nonlinear electrophoretic mobilities of cells and microparticles. Anal. Chem. 92 (22), 14885–14891.CrossRefGoogle ScholarPubMed
Bhattacharyya, S. & Gopmandal, P.P. 2011 Migration of a charged sphere at an arbitrary velocity in an axial electric field. Colloids Surf. (A) 390 (1–3), 86–94.CrossRefGoogle Scholar
Booth, F. 1950 The cataphoresis of spherical, solid non-conducting particles in a symmetrical electrolyte. Proc. R. Soc. Lond. A 203 (1075), 514–533.Google Scholar
Cardenas-Benitez, B., Jind, B., Gallo-Villanueva, R.C., Martinez-Chapa, S.O., Lapizco-Encinas, B.H. & Perez-Gonzalez, V.H. 2020 Direct current electrokinetic particle trapping in insulator-based microfluidics: theory and experiments. Anal. Chem. 92 (19), 12871–12879.CrossRefGoogle ScholarPubMed
Chisholm, N.G., Legendre, D., Lauga, E. & Khair, A.S. 2016 A squirmer across Reynolds numbers. J. Fluid Mech. 796, 233–256.CrossRefGoogle Scholar
De Corato, M., Arqué, X., Patino, T., Arroyo, M., Sánchez, S. & Pagonabarraga, I. 2020 Self-propulsion of active colloids via ion release: theory and experiments. Phys. Rev. Lett. 124 (10), 108001.CrossRefGoogle ScholarPubMed
Debye, P.J.W. & Hückel, E. 1924 Bemerkungen zu einem Satze über die kataphoretische Wanderungsgeschwindigkeit suspendierter Teilchen. Hirzel.Google Scholar
Dukhin, S.S. & Semenikhin, V.N. 1970 Theory of double layer polarization and its influence on the electrokinetic and electro-optical phenomena and the dielectric permeability of disperse systems. Colloid J. USSR 32 (3), 298–305.Google Scholar
Erickson, D. & Li, D. 2004 Integrated microfluidic devices. Anal. Chim. Acta 507 (1), 11–26.CrossRefGoogle Scholar
Fixman, M. & Jagannathan, S. 1983 Spherical macroions in strong fields. Macromolecules 16 (4), 685–699.CrossRefGoogle Scholar
Frants, E.A., Artyukhov, D.A., Kireeva, T.S., Ganchenko, G.S. & Demekhin, E.A. 2021 Vortex formation and separation from the surface of a charged dielectric microparticle in a strong electric field. Fluid Dyn. 56 (1), 134–141.CrossRefGoogle Scholar
Geuzaine, C. & Remacle, J.F. 2009 Gmsh: a 3-D finite element mesh generator with built-in pre- and post-processing facilities. Intl J. Numer. Meth. Engng 79 (11), 1309–1331.CrossRefGoogle Scholar
Henry, D.C. 1931 The cataphoresis of suspended particles. Part I – the equation of cataphoresis. Proc. R. Soc. Lond. A 133 (821), 106–129.Google Scholar
Huang, X.C., Quesada, M.A. & Mathies, R.A. 1992 DNA sequencing using capillary array electrophoresis. Anal. Chem. 64 (18), 2149–2154.CrossRefGoogle ScholarPubMed
Karniadakis, G. & Sherwin, S. 2005 Spectral/HP Element Methods for Computational Fluid Dynamics. Oxford University Press.CrossRefGoogle Scholar
Khair, A.S. 2018 Strong deformation of the thick electric double layer around a charged particle during sedimentation or electrophoresis. Langmuir 34 (3), 876–885.CrossRefGoogle ScholarPubMed
Khair, A.S. & Chisholm, N.G. 2014 Expansions at small Reynolds numbers for the locomotion of a spherical squirmer. Phys. Fluids 26 (1), 011902.CrossRefGoogle Scholar
Kumar, A., Elele, E., Yeksel, M., Khusid, B., Qiu, Z. & Acrivos, A. 2006 Measurements of the fluid and particle mobilities in strong electric fields. Phys. Fluids 18 (12), 123301.CrossRefGoogle Scholar
Liu, P. & Mathies, R.A. 2009 Integrated microfluidic systems for high-performance genetic analysis. Trends Biotechnol. 27 (10), 572–581.CrossRefGoogle ScholarPubMed
Mittal, M., Lele, P.P., Kaler, E.W. & Furst, E.M. 2008 Polarization and interactions of colloidal particles in AC electric fields. J. Chem. Phys. 129 (6), 064513.CrossRefGoogle ScholarPubMed
Morrison, F.A. 1970 Electrophoresis of a particle of arbitrary shape. J. Colloid Interface Sci. 34 (2), 210–214.CrossRefGoogle Scholar
O'Brien, R.W. 1983 The solution of the electrokinetic equations for colloidal particles with thin double layers. J. Colloid Interface Sci. 92 (1), 204–216.CrossRefGoogle Scholar
O'Brien, R.W. & Hunter, R.J. 1981 The electrophoretic mobility of large colloidal particles. Can. J. Chem. 59 (13), 1878–1887.CrossRefGoogle Scholar
O'Brien, R.W. & White, L.R. 1978 Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc. Faraday Trans. 74, 1607–1626.CrossRefGoogle Scholar
Overbeek, J.T.G. 1943 Theory of the relaxation effect in electrophoresis. Kolloide Beihefte 54, 287–364.CrossRefGoogle Scholar
Russel, W.B., Saville, D.A. & Schowalter, W.R. 1991 Colloidal Dispersions. Cambridge University Press.Google Scholar
Schnitzer, O. & Yariv, E. 2012 a Dielectric–solid polarization at strong fields: breakdown of Smoluchowski's electrophoresis formula. Phys. Fluids 24 (8), 082005.CrossRefGoogle Scholar
Schnitzer, O. & Yariv, E. 2012 b Macroscale description of electrokinetic flows at large zeta potentials: nonlinear surface conduction. Phys. Rev. E 86 (2), 021503.CrossRefGoogle ScholarPubMed
Schnitzer, O. & Yariv, E. 2012 c Strong-field electrophoresis. J. Fluid Mech. 701, 333–351.CrossRefGoogle Scholar
Schnitzer, O. & Yariv, E. 2014 Nonlinear electrophoresis at arbitrary field strengths: small-Dukhin-number analysis. Phys. Fluids 26 (12), 122002.CrossRefGoogle Scholar
Schnitzer, O., Zeyde, R., Yavneh, I. & Yariv, E. 2013 Weakly nonlinear electrophoresis of a highly charged colloidal particle. Phys. Fluids 25 (5), 052004.CrossRefGoogle Scholar
Smoluchowski, M. 1903 Contribution à la théorie de l'endosmose électrique et de quelques phénomènes corrélatifs. Bull. Akad. Sci. Cracovie. 8, 182–200.Google Scholar
Stotz, S. 1978 Field dependence of the electrophoretic mobility of particles suspended in low-conductivity liquids. J. Colloid Interface Sci. 65 (1), 118–130.CrossRefGoogle Scholar
Tottori, S., Misiunas, K., Keyser, U.F. & Bonthuis, D.J. 2019 Nonlinear electrophoresis of highly charged nonpolarizable particles. Phys. Rev. Lett. 123 (1), 014502.CrossRefGoogle ScholarPubMed
Vanysek, P. 1993 Ionic Conductivity and Diffusion at Infinite Dilution. CRC Handbook of Chemistry and Physics, pp. 5–92. CRC Press.Google Scholar
Wiersema, P.H., Loeb, A.L. & Overbeek, J.T.G. 1966 Calculation of the electrophoretic mobility of a spherical colloid particle. J. Colloid Interface Sci. 22 (1), 78–99.CrossRefGoogle Scholar
Zhu, Z., Lu, J.J. & Liu, S. 2012 Protein separation by capillary gel electrophoresis: a review. Anal. Chim. Acta 709, 21–31.CrossRefGoogle ScholarPubMed