Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T04:25:42.096Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear interaction of wind-driven oblique surface waves and parametric growth of lower frequency modes

Published online by Cambridge University Press:  12 July 2012

Sang Soo Lee
Sang Soo Lee*
Affiliation:
Naval Surface Warfare Center, Carderock Division, West Bethesda, MD 20817, USA
*
†Email address for correspondence: SangSoo.Lee@navy.mil
Get access Rights & Permissions [Opens in a new window]

Abstract

Nonlinear interactions between free-surface waves of the same wave speed and wind are studied by extending the linear resonant theory of Miles (J. Fluid Mech., vol. 3, 1957, pp. 185–204). A nonlinear interaction can occur when the steepness of a primary three-dimensional wave, which propagates obliquely to the wind direction, becomes of the order of the cube of the density ratio of air to water. If a secondary wave of smaller amplitude is also an oblique wave, the nonlinear critical-layer interaction between the primary and secondary fluctuations in air generates a difference mode whose wavenumbers are equal to the differences between the primary and secondary values. In addition, the nonlinear interaction in the critical layer between the primary and difference modes induces a parametric-growth effect on the secondary surface wave, if the frequency of the primary wave is higher than that of the secondary wave. The primary wave remains linear during this ‘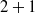 mode critical-layer interaction’ stage between two free-surface waves and a nonlinearly generated mode. The evolution of the secondary-wave amplitude is governed by an integro-differential equation and that of the difference mode is determined by an integral equation. Both inviscid and viscous numerical results show that the nonlinear growth rates become much larger than the linear growth rates. Effect of viscosity is shown to delay the onset of the nonlinear growth. The growth of the secondary and difference modes is more effectively enhanced when the signs of propagation angles of the primary and secondary waves are opposite than when they are equal. The 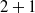mode interaction can occur when wave steepnesses are very small. The nonlinear interaction is entirely confined to a thin critical layer, and the perturbations outside the critical layer are governed by linear equations. It is shown that the initial nonlinear growth of a free-surface wave could be governed by a mode–mode interaction in air.

JFM classification

Waves/Free-surface Flows: Critical layers Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 150 - 190
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alexakis, A., Calder, A. C., Dursi, L. J., Rosner, R., Truran, J. W., Fryxell, B., Zingale, M., Timmes, F. X., Olson, K. & Ricker, P. 2004a On the nonlinear evolution of wind-driven gravity waves. Phys. Fluids 16, 3256–3268.CrossRefGoogle Scholar
2. Alexakis, A., Young, Y. & Rosner, R. 2002 Shear instability of fluid interfaces: stability analysis. Phys. Rev. E 63, 026313.CrossRefGoogle Scholar
3. Alexakis, A., Young, Y.-N. & Rosner, R. 2004b Weakly nonlinear analysis of wind-driven gravity waves. J. Fluid Mech. 503, 171–200.CrossRefGoogle Scholar
4. Benney, D. J. & Bergeron, R. F. Jr. 1969 A new class of nonlinear waves in parallel flows. Stud. Appl. Math. 48, 181–204.CrossRefGoogle Scholar
5. Blennerhassett, P. J. 1980 On the generation of waves by wind. Phil. Trans. R. Soc. Lond. A 298, 451–494.Google Scholar
6. Caulliez, G. & Collard, F. 1999 Three-dimensional evolution of wind waves from gravity-capillary to short gravity range. Eur. J. Mech. B 18, 389–402.CrossRefGoogle Scholar
7. Cavaleri, L. et al. 2007 Wave modelling: the state of the art. Prog. Oceanogr. 75, 603–674.CrossRefGoogle Scholar
8. Charnock, H. 1955 Wind stress on a water surface. Q. J. R. Meteorol. Soc. 81, 639–640.CrossRefGoogle Scholar
9. Conte, S. D. & Miles, J. W. 1959 On the numerical integration of the Orr–Sommerfeld equation. J. Soc. Ind. Appl. Math. 7, 361–366.CrossRefGoogle Scholar
10. Davis, R. E. 1969 On the high Reynolds number flow over a wavy boundary. J. Fluid Mech. 36, 337–346.CrossRefGoogle Scholar
11. Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, second edition. Cambridge University Press.CrossRefGoogle Scholar
12. Fehlberg, E. 1970 Klassiche Runge–Kutta-Formeln vierter und niedrigerer Ordnung mit Schrittweiten-Kontrolle und ihre Anwendung auf Wärmeleitungsprobleme. Computing 6, 61–71.CrossRefGoogle Scholar
13. Forsythe, G. E, Malcolm, M. A. & Moler, C. B. 1977 Computer Methods for Mathematical Computations. Prentice Hall.Google Scholar
14. Goldstein, M. E. 1995 The role of nonlinear critical layers in boundary layer transition. Phil. Trans. R. Soc. Lond. A 352, 425–442.Google Scholar
15. Goldstein, M. E. & Choi, S. W. 1989 Nonlinear evolution of interacting oblique waves on two-dimensional shear layers. J. Fluid Mech. 207, 97–120. Also Corrigendum, J. Fluid Mech. 216, 659–663.CrossRefGoogle Scholar
16. Goldstein, M. E., Durbin, P. A. & Leib, S. J. 1987 Roll-up of vorticity in adverse-pressure-gradient boundary layers. J. Fluid Mech. 183, 325–342.CrossRefGoogle Scholar
17. Goldstein, M. E. & Hultgren, L. S. 1988 Nonlinear spatial evolution of an externally excited instability wave in a free shear layer. J. Fluid Mech. 197, 295–330.CrossRefGoogle Scholar
18. Goldstein, M. E. & Lee, S. S. 1992 Fully coupled resonant-triad interaction in an adverse-pressure-gradient boundary layer. J. Fluid Mech. 245, 523–551.CrossRefGoogle Scholar
19. Goldstein, M. E. & Lee, S. S. 1993 Oblique instability waves in nearly parallel shear flows. In Nonlinear Waves and Weak Turbulence with Applications in Oceanography and Condensed Matter Physics (ed. Fitzmaurice, N., Gurarie, D., McCaughan, F. & Woyczynski, W. ). pp. 159–177. Birkhäuser.CrossRefGoogle Scholar
20. Goldstein, M. E. & Leib, S. J. 1989 Nonlinear evolution of oblique waves on compressible shear layers. J. Fluid Mech. 207, 73–96.CrossRefGoogle Scholar
21. Hristov, T. S., Miller, S. D. & Friehe, C. A. 2003 Dynamical coupling of wind and ocean waves through wave-induced air flow. Nature 442, 55–58.CrossRefGoogle Scholar
22. Hultgren, L. S. 1992 Nonlinear spatial equilibration of an externally excited instability wave in a free shear layer. J. Fluid Mech. 236, 635–664.CrossRefGoogle Scholar
23. Janssen, P. 2004 The Interaction of Ocean Waves and Wind. Cambridge University Press.CrossRefGoogle Scholar
24. Kinsman, B. 1965 Wind Waves, Their Generation and Propagation on the Ocean Surface. Prentice Hall.Google Scholar
25. Komen, G. J., Cavaleri, L., Donelan, M., Hasselmann, K., Hasselmann, S. & Janssen, P. A. E. M. 1994 Dynamics and Modelling of Ocean Waves. Cambridge University Press.CrossRefGoogle Scholar
26. Lee, S. S. 1997 Generalized critical-layer analysis of fully coupled resonant-triad interactions in boundary layers. J. Fluid Mech. 347, 71–103.CrossRefGoogle Scholar
27. Lee, S. S. & Wundrow, D. W. 2011 Transition from long-crested to short-crested seas by wind–wave interaction. In Proceedings of the 21st International Offshore (Ocean) & Polar Engineering Conference, June 19-24, 2011, Maui, HI, vol. 3, pp. 298–305. ISOPE.Google Scholar
28. Lin, C. C. 1945 On the stability of two-dimensional parallel flows. Parts 1, 2, 3. Q. Appl. Math. 3, 117–142 218–234, 277–301.CrossRefGoogle Scholar
29. Miles, J. W. 1957 On the generation of surface waves by shear flows. J. Fluid Mech. 3, 185–204.CrossRefGoogle Scholar
30. Miles, J. W. 1993 Surface-wave generation revisited. J. Fluid Mech. 256, 427–441.CrossRefGoogle Scholar
31. Miles, J. W. 1997 Generation of surface waves by wind. Appl. Mech. Rev. 50, R5-9.CrossRefGoogle Scholar
32. Morland, L. C. & Saffman, P. G. 1993 Effect of wind profile on the instability of wind blowing over water. J. Fluid Mech. 252, 383–398.CrossRefGoogle Scholar
33. Nayfeh, A. H. 1981 Introduction to Perturbation Techniques. Wiley.Google Scholar
34. Phillips, O. M. 1960 On the dynamics of unsteady gravity waves of finite amplitude. Part 1. The elementary interactions. J. Fluid Mech. 9, 193–217.CrossRefGoogle Scholar
35. Reutov, V. P. 1980 The plasma-hydrodynamic analogy and the nonlinear stage of instability of wind waves. Izv. Atmos. Ocean. Phys. 16, 938–943.Google Scholar
36. Sullivan, P. P. & McWilliams, J. C. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.CrossRefGoogle Scholar
37. Valenzuela, G. R. 1976 The growth of gravity-capillary waves in a coupled shear flow. J. Fluid Mech. 76, 229–250.CrossRefGoogle Scholar
38. Wehausen, J. V. & Laitone, E. V. 1960 Surface Waves (ed. Flügge, W. & Truesdell, C. ). Handbuch der Physik , IX, pp. 446–778. Springer.Google Scholar
39. Wu, X. 1992 The nonlinear evolution of high-frequency resonant-triad waves in an oscillatory Stokes layer at high Reynolds number. J. Fluid Mech. 245, 553–597.CrossRefGoogle Scholar
40. Wu, X., Lee, S. S. & Cowley, S. J. 1993 On the weakly nonlinear three-dimensional instability of shear layers to pairs of oblique waves: the Stokes layer as a paradigm. J. Fluid Mech. 253, 681–721.CrossRefGoogle Scholar
41. Wu, X. & Stewart, P. A. 1996 Interaction of phase-locked modes: a new mechanism for the rapid growth of three-dimensional disturbances. J. Fluid Mech. 316, 335–372.CrossRefGoogle Scholar
42. Wu, X., Stewart, P. A. & Cowley, S. J 2007 On the catalytic role of the phase-locked interaction of Tollmien–Schlichting waves in boundary-layer transition. J. Fluid Mech. 590, 265–294.CrossRefGoogle Scholar
43. Wundrow, D. W., Hultgren, L. S. & Goldstein, M. E. 1994 Interaction of oblique instability waves with a nonlinear plane wave. J. Fluid Mech. 264, 343–372.CrossRefGoogle Scholar