Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T22:40:31.321Z Has data issue: false hasContentIssue false
  • English
  • Français

A nonlinear small-deformation theory for transient droplet electrohydrodynamics

Published online by Cambridge University Press:  28 November 2016

Debasish Das  and
David Saintillan
Debasish Das
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
David Saintillan*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
*
†Email address for correspondence: dstn@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The deformation of a viscous liquid droplet suspended in another liquid and subject to an applied electric field is a classic multiphase flow problem best described by the Melcher–Taylor leaky dielectric model. The main assumption of the model is that any net charge in the system is concentrated on the interface between the two liquids as a result of the jump in Ohmic currents from the bulk. Upon application of the field, the drop can either attain a steady prolate or oblate shape with toroidal circulating flows both inside and outside arising from tangential stresses on the interface due to action of the field on the surface charge distribution. Since the pioneering work of Taylor (Proc. R. Soc. Lond. A, vol. 291, 1966, pp. 159–166), there have been numerous computational and theoretical studies to predict the deformations measured in experiments. Most existing theoretical models, however, have either neglected transient charge relaxation or nonlinear charge convection by the interfacial flow. 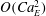In this work, we develop a novel small-deformation theory accurate to second order in electric capillary number $O(Ca_{E}^{2})$ for the complete Melcher–Taylor model that includes transient charge relaxation, charge convection by the flow, as well as transient shape deformation. The main result of the paper is the derivation of coupled evolution equations for the induced electric multipoles and for the shape functions describing the deformations on the basis of spherical harmonics. Our results, which are consistent with previous models in the appropriate limits, show excellent agreement with fully nonlinear numerical simulations based on an axisymmetric boundary element formulation and with existing experimental data in the small-deformation regime.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Drops and Bubbles: Drops Drops and Bubbles: Electrohydrodynamic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 810 , 10 January 2017 , pp. 225 - 253
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK.

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables. Dover.Google Scholar
Ajayi, O. O. 1978 A note on Taylor’s electrohydrodynamic theory. Proc. R. Soc. Lond. A 364, 499–507.Google Scholar
Allan, R. S. & Mason, S. G. 1962 Particle behaviour in shear and electric fields. I. Deformation and burst of fluid drops. Proc. R. Soc. Lond. A 267, 45–61.Google Scholar
Anderson, J. L. 1985 Droplet interactions in thermocapillary motion. Intl J. Multiphase Flow 11, 813–824.CrossRefGoogle Scholar
Bandopadhyay, A., Mandal, S., Kishore, N. K. & Chakraborty, S. 2016 Uniform electric-field-induced lateral migration of a sedimenting drop. J. Fluid Mech. 792, 553–589.Google Scholar
Basaran, O. A., Gao, H. & Bhat, P. P. 2013 Nonstandard inkjets. Annu. Rev. Fluid Mech. 45, 85–113.CrossRefGoogle Scholar
Baygents, J. C., Rivette, N. J. & Stone, H. A. 1998 Electrohydrodynamic deformation and interaction of drop pairs. J. Fluid Mech. 368, 359–375.CrossRefGoogle Scholar
Castellanos, A. 2014 Electrohydrodynamics. Springer.Google Scholar
Collins, R. T., Jones, J. J., Harris, M. T. & Basaran, O. A. 2008 Electrohydrodynamic tip streaming and emission of charged drops from liquid cones. Nat. Phys. 4, 149–154.CrossRefGoogle Scholar
Collins, R. T., Sambath, K., Harris, M. T. & Basaran, O. A. 2013 Universal scaling laws for the disintegration of electrified drops. Proc. Natl Acad. Sci. USA 110, 4905–4910.Google Scholar
Das, D. & Saintillan, D. 2013 Electrohydrodynamic interaction of spherical particles under Quincke rotation. Phys. Rev. E 87, 043014.Google Scholar
Esmaeeli, A. & Sharifi, P. 2011 Transient electrohydrodynamics of a liquid drop. Phys. Rev. E 84, 036308.Google Scholar
Feng, J. Q. 1999 Electrohydrodynamic behaviour of a drop subjected to a steady uniform electric field at finite electric Reynolds number. Proc. R. Soc. Lond. A 455, 2245–2269.Google Scholar
Ha, J.-W. & Yang, S.-M. 2000 Deformation and breakup of Newtonian and non-Newtonian conducting drops in an electric field. J. Fluid Mech. 405, 131–156.CrossRefGoogle Scholar
Harris, F. E. & O’Konski, C. T. 1957 Dielectric properties of aqueous ionic solutions at microwave frequencies. J. Phys. Chem. 61, 310–319.CrossRefGoogle Scholar
Haywood, R. J., Renksizbulut, M. & Raithby, G. D. 1991 Transient deformation of freely-suspended liquid droplets in electrostatic fields. AIChE J. 37, 1305–1317.Google Scholar
He, H., Salipante, P. F. & Vlahovska, P. M. 2013 Electrorotation of a viscous droplet in a uniform direct current electric field. Phys. Fluids 25, 032106.Google Scholar
Huang, Z.-M., Zhang, Y.-Z., Kotaki, M. & Ramakrishna, S. 2003 A review on polymer nanofibers by electrospinning and their applications in nanocomposites. Compos. Sci. Technol. 63, 2223–2253.Google Scholar
Jaswon, M. A. 1963 Integral equation methods in potential theory. I. Proc. R. Soc. Lond. A 275, 23–32.Google Scholar
Joseph, D. D. 1967 Parameter and domain dependence of eigenvalues of elliptic partial differential equations. Arch. Rat. Mech. Anal. 24, 325–351.Google Scholar
Kim, S. & Karrila, S. J. 2013 Microhydrodynamics: Principles and Selected Applications. Dover.Google Scholar
Lac, E. & Homsy, G. M. 2007 Axisymmetric deformation and stability of a viscous drop in a steady electric field. J. Fluid Mech. 590, 239–264.Google Scholar
Lanauze, J. A., Walker, L. M. & Khair, A. S. 2013 The influence of inertia and charge relaxation on electrohydrodynamic drop deformation. Phys. Fluids 25, 112101.Google Scholar
Lanauze, J. A., Walker, L. M. & Khair, A. S. 2015 Nonlinear electrohydrodynamics of slightly deformed oblate drops. J. Fluid Mech. 774, 245–266.Google Scholar
Laser, D. J. & Santiago, J. G. 2004 A review of micropumps. J. Micromech. Microengng 14, R35.CrossRefGoogle Scholar
Leveque, R. J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.Google Scholar
López-Herrera, J. M., Popinet, S. & Herrada, M. A. 2011 A charge-conservative approach for simulating electrohydrodynamic two-phase flows using volume-of-fluid. J. Comput. Phys. 230, 1939–1955.Google Scholar
Melcher, J. R. & Taylor, G. I. 1969 Electrohydrodynamics: a review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1, 111–146.Google Scholar
Moriya, S., Adachi, K. & Kotaka, T. 1986 Deformation of droplets suspended in viscous media in an electric field. I. Rate of deformation. Langmuir 2, 155–160.Google Scholar
O’Konski, C. T. & Thacher, H. C. 1953 The distortion of aerosol droplets by an electric field. J. Phys. Chem. 57, 955–958.Google Scholar
Park, J.-U., Hardy, M., Kang, S. J., Barton, K., Adair, K., Mukhopadhyay, D. K., Lee, C. Y., Strano, M. S., Alleyne, A. G., Georgiadis, J. G., Ferreira, P. M. & Rogers, J. A. 2007 High-resolution electrohydrodynamic jet printing. Nat. Mater. 6, 782–789.Google Scholar
Pelekasis, N. A., Tsamopoulos, J. A. & Manolis, G. D. 1990 Equilibrium shapes and stability of charged and conducting drops. Phys. Fluids 2, 1328–1340.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Pozrikidis, C. 2002 A Practical Guide to Boundary Element Methods with the Software Library BEMLIB. CRC Press.Google Scholar
Pozrikidis, C. 2011 Introduction to Theoretical and Computational Fluid Dynamics. Oxford University Press.Google Scholar
Rallison, J. 1984 The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 16, 45–66.Google Scholar
Salipante, P. F. & Vlahovska, P. M. 2010 Electrohydrodynamics of drops in strong uniform dc electric fields. Phys. Fluids 22, 112110.Google Scholar
Salipante, P. F. & Vlahovska, P. M. 2013 Electrohydrodynamic rotations of a viscous droplet. Phys. Rev. E 88, 043003.Google ScholarPubMed
Saville, D. A. 1997 Electrohydrodynamics: the Taylor–Melcher leaky dielectric model. Annu. Rev. Fluid Mech. 29, 27–64.Google Scholar
Scott, T. C. 1989 Use of electric fields in solvent extraction: a review and prospectus. Sep. Purif. Meth. 18, 65–109.Google Scholar
Sellier, A. 2006 On the computation of the derivatives of potentials on a boundary by using boundary-integral equations. Comput. Meth. Appl. Mech. Engng 196, 489–501.CrossRefGoogle Scholar
Sherwood, J. D. 1988 Breakup of fluid droplets in electric and magnetic fields. J. Fluid Mech. 188, 133–146.Google Scholar
Shkadov, V. Y. & Shutov, A. A. 2002 Drop and bubble deformation in an electric field. Fluid Dyn. 37, 713–724.Google Scholar
Shutov, A. A. 2002 The shape of a drop in a constant electric field. Tech. Phys. 47, 1501–1508.CrossRefGoogle Scholar
Supeene, G., Koch, C. R. & Bhattacharjee, S. 2008 Deformation of a droplet in an electric field: nonlinear transient response in perfect and leaky dielectric media. J. Colloid Interface Sci. 318, 463–476.Google Scholar
Symm, G. T. 1963 Integral equation methods in potential theory. II. Proc. R. Soc. Lond. A 275, 33–46.Google Scholar
Taylor, G. I. 1964 Disintegration of water drops in an electric field. Proc. R. Soc. Lond. A 280, 383–397.Google Scholar
Taylor, G. I. 1966 Studies in electrohydrodynamics. I. The circulation produced in a drop by electrical field. Proc. R. Soc. Lond. A 291, 159–166.Google Scholar
Taylor, G. I. 1969 Electrically driven jets. Proc. R. Soc. Lond. A 313, 453–475.Google Scholar
Tsamopoulos, J. A., Akylas, T. R. & Brown, R. A. 1985 Dynamics of charged drop break-up. Proc. R. Soc. Lond. A 401, 67–88.Google Scholar
Tsukada, T., Katayama, T., Ito, Y. & Hozawa, M. 1993 Theoretical and experimental studies of circulations inside and outside a deformed drop under a uniform electric field. J. Chem. Engng Japan 26, 698–703.Google Scholar
Wilson, C. T. R. & Taylor, G. I. 1925 The bursting of soap-bubbles in a uniform electric field. Math. Proc. Cambridge Philos. Soc. 22, 728–730.Google Scholar
Yariv, E. & Almog, Y. 2016 The effect of surface-charge convection on the settling velocity of spherical drops in a uniform electric field. J. Fluid Mech. 797, 536–548.Google Scholar
Yariv, E. & Frankel, I. 2016 Electrohydrodynamic rotation of drops at large electric Reynolds numbers. J. Fluid Mech. 788, R2.Google Scholar
Zhang, J., Zahn, J. D. & Lin, H. 2013 Transient solution for droplet deformation under electric fields. Phys. Rev. E 87, 043008.Google Scholar

Das and Saintillan supplementary movie

Movie showing the drop deformation and streamlines in the case of system 1b (corresponding to figure 4).

Download Das and Saintillan supplementary movie(Video)
Video 9 MB

Das and Saintillan supplementary movie

Movie showing the drop deformation and velocity field in the case of system 1b (corresponding to figure 4).

Download Das and Saintillan supplementary movie(Video)
Video 4.7 MB