Article contents
Numerical simulation of shear-induced instabilities in internal solitary waves
Published online by Cambridge University Press: 22 August 2011
Abstract
A numerical method that employs a combination of contour advection and pseudo-spectral techniques is used to simulate shear-induced instabilities in an internal solitary wave (ISW). A three-layer configuration for the background stratification, in which a linearly stratified intermediate layer is sandwiched between two homogeneous ones, is considered throughout. The flow is assumed to satisfy the inviscid, incompressible, Oberbeck–Boussinesq equations in two dimensions. Simulations are initialized by fully nonlinear, steady-state, ISWs. The results of the simulations show that the instability takes place in the pycnocline and manifests itself as Kelvin–Helmholtz billows. The billows form near the trough of the wave, subsequently grow and disturb the tail. Both the critical Richardson number (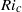 ) and the critical amplitude required for instability are found to be functions of the ratio of the undisturbed layer thicknesses. It is shown, therefore, that the constant, critical bound for instability in ISWs given in Barad & Fringer (J. Fluid Mech., vol. 644, 2010, pp. 61–95), namely
) and the critical amplitude required for instability are found to be functions of the ratio of the undisturbed layer thicknesses. It is shown, therefore, that the constant, critical bound for instability in ISWs given in Barad & Fringer (J. Fluid Mech., vol. 644, 2010, pp. 61–95), namely 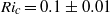 , is not a sufficient condition for instability. It is also shown that the critical value of
, is not a sufficient condition for instability. It is also shown that the critical value of 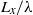 required for instability, where
required for instability, where 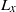 is the length of the region in a wave in which
is the length of the region in a wave in which 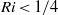 and
and 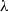 is the half-width of the wave, is sensitive to the ratio of the layer thicknesses. Similarly, a linear stability analysis reveals that
is the half-width of the wave, is sensitive to the ratio of the layer thicknesses. Similarly, a linear stability analysis reveals that 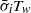 (where
(where 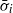 is the growth rate of the instability averaged over
is the growth rate of the instability averaged over 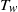 , the period in which parcels of fluid are subjected to
, the period in which parcels of fluid are subjected to 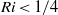 ) is very sensitive to the transition between the undisturbed pycnocline and the homogeneous layers, and the amplitude of the wave. Therefore, the alternative tests for instability presented in Fructus et al. (J. Fluid Mech., vol. 620, 2009, pp. 1–29) and Barad & Fringer (J. Fluid Mech., vol. 644, 2010, pp. 61–95), respectively, namely
) is very sensitive to the transition between the undisturbed pycnocline and the homogeneous layers, and the amplitude of the wave. Therefore, the alternative tests for instability presented in Fructus et al. (J. Fluid Mech., vol. 620, 2009, pp. 1–29) and Barad & Fringer (J. Fluid Mech., vol. 644, 2010, pp. 61–95), respectively, namely 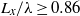 and
and 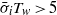 , are shown to be valid only for a limited parameter range.
, are shown to be valid only for a limited parameter range.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
Carr et al. supplementary movie
Movie 1. Evolution of the vorticity field for the wave depicted in figure 2 of the manuscript. The wave is defined as stable, little or no disturbance of the pycnocline is seen
Carr et al. supplementary movie
Movie 1. Evolution of the vorticity field for the wave depicted in figure 2 of the manuscript. The wave is defined as stable, little or no disturbance of the pycnocline is seen
Carr et al. supplementary movie
Movie 2. Evolution of the buoyancy field for the wave depicted in figure 3 of the manuscript. The wave is defined as stable, little or no disturbance of the pycnocline is seen.
Carr et al. supplementary movie
Movie 2. Evolution of the buoyancy field for the wave depicted in figure 3 of the manuscript. The wave is defined as stable, little or no disturbance of the pycnocline is seen.
Carr et al. supplementary movie
Movie 3. Evolution of the vorticity field for the wave depicted in figure 4 of the manuscript. The wave is defined as weakly unstable. Oscillation of the pycnocline is seen but no persistent coherent billows are formed.
Carr et al. supplementary movie
Movie 3. Evolution of the vorticity field for the wave depicted in figure 4 of the manuscript. The wave is defined as weakly unstable. Oscillation of the pycnocline is seen but no persistent coherent billows are formed.
Carr et al. supplementary movie
Movie 4. Evolution of the buoyancy field for the wave depicted in figure 5 of the manuscript. The wave is defined as weakly unstable. Oscillation of the pycnocline is seen but no persistent coherent billows are formed
Carr et al. supplementary movie
Movie 4. Evolution of the buoyancy field for the wave depicted in figure 5 of the manuscript. The wave is defined as weakly unstable. Oscillation of the pycnocline is seen but no persistent coherent billows are formed
Carr et al. supplementary movie
Movie 5. Evolution of the vorticity field for the wave depicted in figure 6 of the manuscript. The wave is defined as unstable. Coherent billows are seen in the pycnocline
Carr et al. supplementary movie
Movie 5. Evolution of the vorticity field for the wave depicted in figure 6 of the manuscript. The wave is defined as unstable. Coherent billows are seen in the pycnocline
- 22
- Cited by


