Article contents
Numerical study of the effect of blockage ratio in forced convection confined flows of shear-thinning fluids
Published online by Cambridge University Press: 27 October 2021
Abstract
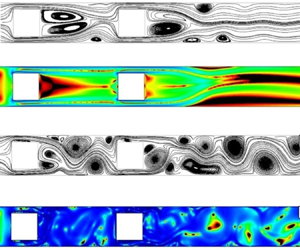
In this work, the fluid dynamics and heat transfer of time-dependent flows with shear-thinning behaviour over two confined square cylinders in tandem arrangement are studied numerically. The case studies include two- and three-dimensional flows under a wide range of power-law indices,  $0.25\leq n \leq 1.0$, and blockage ratios,
$0.25\leq n \leq 1.0$, and blockage ratios,  $\beta =0.50$, 0.66 and 0.80, for a fixed Reynolds number of
$\beta =0.50$, 0.66 and 0.80, for a fixed Reynolds number of  $Re=100$ and Prandtl number of
$Re=100$ and Prandtl number of  $Pr=10$. The fluid dynamic analysis includes detailed qualitative and quantitative comparisons between the different fluids and blockage ratios, where streamlines, viscosity fields, and lift and drag coefficients are presented. Moreover, a detailed study of the route from laminar time-dependent to chaotic flows is included. It was determined that the flow exhibits a transition from laminar to chaotic by decreasing the power-law index (
$Pr=10$. The fluid dynamic analysis includes detailed qualitative and quantitative comparisons between the different fluids and blockage ratios, where streamlines, viscosity fields, and lift and drag coefficients are presented. Moreover, a detailed study of the route from laminar time-dependent to chaotic flows is included. It was determined that the flow exhibits a transition from laminar to chaotic by decreasing the power-law index ( $n$) and increasing the blockage ratio (
$n$) and increasing the blockage ratio ( $\beta$). With respect to the thermal analysis, isotherms and Nusselt numbers are compared between the different case studies. This analysis demonstrates that the average Nusselt numbers increased in chaotic flows. The three-dimensional cases confirmed the results proposed for the two-dimensional case.
$\beta$). With respect to the thermal analysis, isotherms and Nusselt numbers are compared between the different case studies. This analysis demonstrates that the average Nusselt numbers increased in chaotic flows. The three-dimensional cases confirmed the results proposed for the two-dimensional case.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by


