Article contents
A numerical study of turbulence under temporally evolving axisymmetric contraction and subsequent relaxation
Published online by Cambridge University Press: 22 September 2016
Abstract
Direct numerical simulations using up to 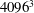 $4096^{3}$ grid points on a deforming domain have been used to study the response of initially isotropic turbulence to a period of spatially uniform axisymmetric contraction (with one extensional and two equally compressive directions) and subsequent relaxation. A time-dependent strain rate is formulated to closely correspond to the downstream evolution in the wind tunnel experiments of Ayyalasomayajula & Warhaft (J. Fluid Mech., vol. 566, 2006, pp. 273–307), with a smoothly varying 4 : 1 contraction ratio. The application of strain leads to anisotropy in both the large scales and the small scales, in a manner where nonlinear effects not considered in rapid-distortion theory play an important role. Upon termination of strain, the small scales quickly return to isotropy while a residual level of anisotropy appears to persist at the large scales. The simulations are shown to reproduce many key findings from experiments, including distinctive changes in the form of the one-dimensional spectra in the extensional direction that arise at sufficiently high Reynolds number, during both the straining and relaxation periods. Scale-dependent measures of anisotropy are presented in terms of one-dimensional spectra and axisymmetric versions of the energy spectrum. To explain the observed changes in spectral shapes, various terms in the spectral evolution equation representing rapid pressure strain, slow pressure strain, production, nonlinear transfer and viscous dissipation are computed, showing that nonlinear effects take a dominant role when a wide range of scales exists. In particular, the ‘double-peak’ spectral form observed in experiments at high Reynolds number is found to be a consequence of the small scales relaxing towards isotropy much faster than the large scales. A comparison of results obtained from computational domains of varying sizes and grid resolutions show that the numerical findings are robust.
$4096^{3}$ grid points on a deforming domain have been used to study the response of initially isotropic turbulence to a period of spatially uniform axisymmetric contraction (with one extensional and two equally compressive directions) and subsequent relaxation. A time-dependent strain rate is formulated to closely correspond to the downstream evolution in the wind tunnel experiments of Ayyalasomayajula & Warhaft (J. Fluid Mech., vol. 566, 2006, pp. 273–307), with a smoothly varying 4 : 1 contraction ratio. The application of strain leads to anisotropy in both the large scales and the small scales, in a manner where nonlinear effects not considered in rapid-distortion theory play an important role. Upon termination of strain, the small scales quickly return to isotropy while a residual level of anisotropy appears to persist at the large scales. The simulations are shown to reproduce many key findings from experiments, including distinctive changes in the form of the one-dimensional spectra in the extensional direction that arise at sufficiently high Reynolds number, during both the straining and relaxation periods. Scale-dependent measures of anisotropy are presented in terms of one-dimensional spectra and axisymmetric versions of the energy spectrum. To explain the observed changes in spectral shapes, various terms in the spectral evolution equation representing rapid pressure strain, slow pressure strain, production, nonlinear transfer and viscous dissipation are computed, showing that nonlinear effects take a dominant role when a wide range of scales exists. In particular, the ‘double-peak’ spectral form observed in experiments at high Reynolds number is found to be a consequence of the small scales relaxing towards isotropy much faster than the large scales. A comparison of results obtained from computational domains of varying sizes and grid resolutions show that the numerical findings are robust.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 9
- Cited by


