Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-14T03:09:28.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Obtaining accurate mean velocity measurements in high Reynolds number turbulent boundary layers using Pitot tubes

Published online by Cambridge University Press:  09 January 2013

S. C. C. Bailey ,
M. Hultmark ,
J. P. Monty ,
P. H. Alfredsson ,
M. S. Chong ,
R. D. Duncan ,
J. H. M. Fransson ,
N. Hutchins ,
I. Marusic  and
B. J. McKeon
...Show all authors
S. C. C. Bailey*
Affiliation:
Department of Mechanical Engineering, University of Kentucky, Lexington, KY 40506, USA
M. Hultmark
Affiliation:
Deparment of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
J. P. Monty
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
P. H. Alfredsson
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
M. S. Chong
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
R. D. Duncan
Affiliation:
Illinois Institute of Technology, Chicago, IL 60616, USA
J. H. M. Fransson
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
N. Hutchins
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
I. Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
B. J. McKeon
Affiliation:
Graduate Aeronautical Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
H. M. Nagib
Affiliation:
Illinois Institute of Technology, Chicago, IL 60616, USA
R. Örlü
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
A. Segalini
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden II Facoltà di Ingegneria, Università di Bologna, I-47100 Forlí, Italy
A. J. Smits
Affiliation:
Deparment of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
R. Vinuesa
Affiliation:
Illinois Institute of Technology, Chicago, IL 60616, USA
*
†Email address for correspondence: scbailey@engr.uky.EDU
Get access Rights & Permissions [Opens in a new window]

Abstract

This article reports on one component of a larger study on measurement of the zero-pressure-gradient turbulent flat plate boundary layer, in which a detailed investigation was conducted of the suite of corrections required for mean velocity measurements performed using Pitot tubes. 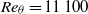In particular, the corrections for velocity shear across the tube and for blockage effects which occur when the tube is in close proximity to the wall were investigated using measurements from Pitot tubes of five different diameters, in two different facilities, and at five different Reynolds numbers ranging from ${\mathit{Re}}_{\theta } = 11\hspace{0.167em} 100$ to 67 000. Only small differences were found amongst commonly used corrections for velocity shear, but improvements were found for existing near-wall proximity corrections. Corrections for the nonlinear averaging of the velocity fluctuations were also investigated, and the results compared to hot-wire data taken as part of the same measurement campaign. The streamwise turbulence-intensity correction was found to be of comparable magnitude to that of the shear correction, and found to bring the hot-wire and Pitot results into closer agreement when applied to the data, along with the other corrections discussed and refined here.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 642 - 670
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chue, S. H. 1975 Pressure probes for fluid measurement. Prog. Aerosp. Sci. 16 (2), 147–223.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
Dickinson, J. 1975 Turbulent skin friction techniques. Tech. Rep. Laval University, Quebec.Google Scholar
Goldstein, S. 1938 Modern developments in fluid dynamics. Proc. R. Soc. Lond. 155, 570–575.Google Scholar
Hall, I. M. 1956 The displacement effect of a sphere in two-dimensional shear flow. J. Fluid Mech. 1, 142–162.CrossRefGoogle Scholar
Hites, M. H. 1997 Scaling of high-Reynolds number turbulent boundary layers in the National Diagnostic Facility. PhD thesis, Illinois Institiute of Technology.Google Scholar
Hoffman, K. A. & Chiang, S. T. 2000 Computational Fluid Dynamics, 4th edn, vol. I, Engineering Education System.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. A 365, 647–664.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635 (1), 103–136.Google Scholar
Lighthill, M. J. 1957 Contributions to the theory of the Pitot-tube displacement effect. J. Fluid Mech. 2, 493–512.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5 (6), 407–417.Google Scholar
Lindgren, B. & Johansson, A. V. 2002 Evaluation of the flow quality in the MTL wind-tunnel. Tech. Rep. 2002:13, Department of Mechanics, KTH, Stockholm, Sweden.Google Scholar
MacMillan, F. A. 1954 Viscous effects on Pitot tubes at low speeds. J. R. Aero. Soc. 58, 837–839.Google Scholar
MacMillan, F. A. 1957 Experiments on Pitot tubes in shear flow. Ministry of Supply, Aero. Res. Council 3028.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
McKeon, B. J. 2007 Pressure-based velocity measurements. In Springer Handbook of Experimental Fluid Mechanics, pp. 216–229. Springer.Google Scholar
McKeon, B. J., Li, J., Jiang, W, Morrison, J. F. & Smits, A. J. 2003 Pitot probe corrections in fully developed turbulent pipe flow. Meas. Sci. Technol. 14, 1449–1458.Google Scholar
McKeon, B. J. & Smits, A. J. 2002 Static pressure correction in high Reynolds number fully developed turbulent pipe flow. Meas. Sci. Technol. 13, 1608–1614.Google Scholar
Metzger, M. M., Klewicki, J. C., Bradshaw, K. L. & Sadr, R. 2001 Scaling the near-wall axial turbulent stress in the zero pressure gradient boundary layer. Phys. Fluids 13 (6), 1819–1821.Google Scholar
Mochizuki, S. & Nieuwstadt, F. T. M. 1996 Reynolds-number-dependence of the maximum in the streamwise velocity fluctuations in wall turbulence. Exp. Fluids 21, 218–226.Google Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. A 365, 807–822.CrossRefGoogle ScholarPubMed
Örlü, R. & Alfredsson, P. H. 2010 On spatial resolution issues related to time-averaged quantities using hot-wire anemometry. Exp. Fluids 49, 101–110.CrossRefGoogle Scholar
Örlü, R., Fransson, J. H. M. & Alfredsson, P. H. 2010 On near wall measurements of wall bounded flows: the necessity of an accurate determination of the wall position. Prog. Aerosp. Sci. 46, 353–387.Google Scholar
Österlund, J. M. 1999 Experimental studies of zero pressure-gradient turbulent boundary layer flow. PhD thesis, KTH, Stockholm, Sweden.Google Scholar
Ozarapoglu, V. 1973 Measurements in incompressible turbulent flows. PhD thesis, Laval University.Google Scholar
Patel, V. C. 1965 Calibration of the Preston tube and limitations on its use in pressure gradients. J. Fluid Mech. 23, 185–208.Google Scholar
Perry, A. E., Hafez, S. & Chong, M. S. 2001 A possible reinterpretation of the Princeton superpipe data. J. Fluid Mech. 439, 395–401.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Tavoularis, S. 2005 Measurement in Fluid Mechanics. Cambridge University Press.Google Scholar
Tavoularis, S. & Szymczak, M. 1989 Displacement effect of square-ended tubes in shear flows. Exp. Fluids 7, 33–37.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.Google Scholar