Published online by Cambridge University Press: 18 December 2013
Motivated by experiments showing that a sessile drop of volatile perfectly wetting liquid initially advances over the substrate, but then reverses, we formulate the problem describing the contact region at reversal. Assuming a separation of scales, so that the radial extent of this region is small compared with the instantaneous radius  $a$ of the apparent contact line, we show that the time scale characterizing the contact region is small compared with that on which the bulk drop is evolving. As a result, the contact region is governed by a boundary-value problem, rather than an initial-value problem: the contact region has no memory, and all its properties are determined by conditions at the instant of reversal. We conclude that the apparent contact angle
$a$ of the apparent contact line, we show that the time scale characterizing the contact region is small compared with that on which the bulk drop is evolving. As a result, the contact region is governed by a boundary-value problem, rather than an initial-value problem: the contact region has no memory, and all its properties are determined by conditions at the instant of reversal. We conclude that the apparent contact angle 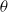 $\theta $ is a function of the instantaneous drop radius
$\theta $ is a function of the instantaneous drop radius  $a$, as found in the experiments. We then non-dimensionalize the boundary-value problem, and find that its solution depends on one parameter
$a$, as found in the experiments. We then non-dimensionalize the boundary-value problem, and find that its solution depends on one parameter 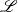 $\mathscr{L}$, a dimensionless surface tension. According to this formulation, the apparent contact angle is well-defined: at the outer edge of the contact region, the film slope approaches a limit that is independent of the curvature of bulk drop. In this, it differs from the dynamic contact angle observed during spreading of non-volatile drops. Next, we analyse the boundary-value problem assuming
$\mathscr{L}$, a dimensionless surface tension. According to this formulation, the apparent contact angle is well-defined: at the outer edge of the contact region, the film slope approaches a limit that is independent of the curvature of bulk drop. In this, it differs from the dynamic contact angle observed during spreading of non-volatile drops. Next, we analyse the boundary-value problem assuming 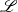 $\mathscr{L}$ to be small. Though, for arbitrary
$\mathscr{L}$ to be small. Though, for arbitrary 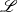 $\mathscr{L}$, determining
$\mathscr{L}$, determining 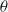 $\theta $ requires solving the steady diffusion equation for the vapour, there is, for small
$\theta $ requires solving the steady diffusion equation for the vapour, there is, for small 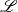 $\mathscr{L}$, a further separation of scales within the contact region. As a result,
$\mathscr{L}$, a further separation of scales within the contact region. As a result, 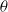 $\theta $ is now determined by solving an ordinary differential equation. We predict that
$\theta $ is now determined by solving an ordinary differential equation. We predict that 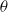 $\theta $ varies as
$\theta $ varies as 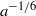 ${a}^{- 1/ 6} $, as found experimentally for small drops (
${a}^{- 1/ 6} $, as found experimentally for small drops (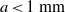 $a\lt 1~\mathrm{mm} $). For these drops, predicted and measured angles agree to within 10–30 %. Because the discrepancy increases with
$a\lt 1~\mathrm{mm} $). For these drops, predicted and measured angles agree to within 10–30 %. Because the discrepancy increases with  $a$, but
$a$, but 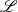 $\mathscr{L}$ is a decreasing function of
$\mathscr{L}$ is a decreasing function of  $a$, we infer that some process occurring outside the contact region is required to explain the observed behaviour of larger drops having
$a$, we infer that some process occurring outside the contact region is required to explain the observed behaviour of larger drops having 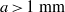 $a\gt 1~\mathrm{mm} $.
$a\gt 1~\mathrm{mm} $.