Article contents
On the response of convectively unstable flows to oscillatory forcing with application to liquid sheets
Published online by Cambridge University Press: 19 April 2012
Abstract
The complete integral solution is found for the convectively unstable and oscillatory-forced linear Klein–Gordon equation as a function of spatial variable,  , and time,
, and time,  . A comparison of the integral solution with series solutions of the Klein–Gordon equation elucidates salient features of both the transient and long-time spatially growing solutions. A rigorous method is developed for identifying the key
. A comparison of the integral solution with series solutions of the Klein–Gordon equation elucidates salient features of both the transient and long-time spatially growing solutions. A rigorous method is developed for identifying the key 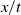 rays associated with saddle points that can be used to characterize the transition between transient temporally growing and long-term spatially growing waves. This method effectively combines the procedure given by Gordillo & Pérez-Saborid (Phys. Fluids, vol. 14, 2002, pp. 4329–4343) for determining the
rays associated with saddle points that can be used to characterize the transition between transient temporally growing and long-term spatially growing waves. This method effectively combines the procedure given by Gordillo & Pérez-Saborid (Phys. Fluids, vol. 14, 2002, pp. 4329–4343) for determining the 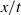 ray at which the forced spatial growth response affects the observed waveform and competes with the transient response, with an established methodology for identifying the leading and trailing edge rays of an impulse response. The method is applied to a linearized system describing an oscillatory-forced liquid sheet and asymptotic predictions are obtained. Series solutions are used to validate these predictions. We establish that the portion of the solution responsible for spatial growth in the signalling problem is correctly identified by Gordillo & Pérez-Saborid (Phys. Fluids, vol. 14, 2002, pp. 4329–4343), and that this interpretation is in contrast with the classical literature. The approach provided here can be applied in multiple ways to study a convectively unstable oscillatory-forced medium. In cases where numerical or series solutions are readily available, the proposed method is used to extract key features of the solution. In cases where only the forced long time behaviour is needed, the dispersion relation is used to extract: (i) the time required to see the forced solution; (ii) the amplitude, phase and spatial growth of the forced solution; and (iii) the breadth of the transient.
ray at which the forced spatial growth response affects the observed waveform and competes with the transient response, with an established methodology for identifying the leading and trailing edge rays of an impulse response. The method is applied to a linearized system describing an oscillatory-forced liquid sheet and asymptotic predictions are obtained. Series solutions are used to validate these predictions. We establish that the portion of the solution responsible for spatial growth in the signalling problem is correctly identified by Gordillo & Pérez-Saborid (Phys. Fluids, vol. 14, 2002, pp. 4329–4343), and that this interpretation is in contrast with the classical literature. The approach provided here can be applied in multiple ways to study a convectively unstable oscillatory-forced medium. In cases where numerical or series solutions are readily available, the proposed method is used to extract key features of the solution. In cases where only the forced long time behaviour is needed, the dispersion relation is used to extract: (i) the time required to see the forced solution; (ii) the amplitude, phase and spatial growth of the forced solution; and (iii) the breadth of the transient.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 8
- Cited by

