Article contents
On the starting vortex generated by a translating and rotating flat plate
Published online by Cambridge University Press: 10 November 2020
Abstract
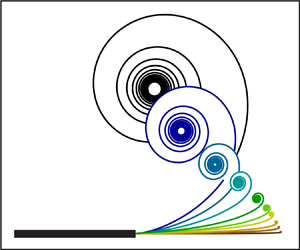
We consider the trailing-edge vortex produced in an inviscid fluid by the start-up motion of a two-dimensional flat plate. A general starting motion is studied that includes the initial angle-of-attack of the plate (which may be zero), individual time power laws for plate translational and rotational speeds and the pivot position for plate rotation. A vortex-sheet representation for a start-up separated flow at the trailing edge is developed whose time-wise evolution is described by a Birkhoff–Rott equation coupled to an appropriate Kutta condition. This description includes convection by the outer flow, rotation and vortex-image self-induction. It admits a power-law similarity solution for the (small-time) primitive vortex, leading to an equation set where each term carries its own time-wise power-law factor. A set of four general plate motions is defined. Dominant-balance analysis of this set leads to discovery of three distinct start-up vortex-structure types that form the basis for all vortex motion. The properties of each type are developed in detail for some special cases. Numerical and analytical solutions are described and transition between solution types is discussed. Singular and degenerate vortex behaviour is discovered which may be due to the absence of fluid viscosity. An interesting case is start-up motion with zero initial angle of attack coupled to power-law plate rotation for which time-series examples are given that can be compared to high Reynolds number viscous flows.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 8
- Cited by


